Галилей-инвариантность современной физики

Сразу введу в курс дела. Галилей-инвариантность – это когда вне зависимости от того, смотреть ли за каким-то процессом с едущего равномерно и прямолинейно поезда, или стоять прямо около происходящего, законы физики будут одинаковыми. Т.е. если два упругих шарика сталкиваются, то результат расчёта этого взаимодействия по известным формулам будет одинаков хоть с позиции движущегося инерционно наблюдателя, хоть с позиции покоящегося. Не будет никаких дополнительных членов в законах и уравнениях. Это логично и естественно. Ведь мир объективно существует, а законы едины и строги.

Но есть такое поверье в современной физике, что электромагнетизм не подчиняется так называемой Галилей-инвариантности. (На самом деле не только электромагнетизм, а вообще всё, но об этом позже.) Т.е. если считать, что мир привычен нашему опыту, то с электродинамикой будут проблемы, ведь она Лоренц-инвариантна. Как-то на пальцах объяснить, что именно под этим подразумевается, сложно. Но можно объяснить чисто формально, математически. Если в любых формулах для вычисления ускорения или силы заменить переменные, описывающие движение, в соответствии с некоторым преобразованием, то вид этих формул никак не изменится. Для Галилей-инвариантности будут простые преобразования вида v’=v+Δv, где v’ – это новая переменная скорости, v – старая переменная скорости, а Δv – некоторая постоянная добавка. А для Лоренц-инвариантности будет преобразование Лоренца:

Теперь рассмотрим два одноимённо заряженных тела, покоящихся относительно друг друга. Если они стоят на месте, они отталкиваются по Кулону. Но если они начнут двигаться, то в зависимости от скорости может наступить даже такое состояние, что они начнут притягиваться из-за возникшего магнитного поля. Можно сформулировать множество подобных экспериментов, общая суть которых будет одинаковой – принцип относительности не соблюдается. Это утверждение могло быть опровержением принципа относительности Эйнштейна, но учёные поступили хитрее, они назвали это обстоятельство чисто релятивистским эффектом. Т.е. мало того, что описанная ситуация не удовлетворяет принятой теории, так это ещё и провозглашается квинтэссенцией теории относительности. Логика сложно прослеживается, но оставим это за скобками.

В свою очередь если между этими зарядами есть какая-то среда, движение относительно которой и воспроизводит эти якобы чисто релятивистские эффекты, то принцип относительности не нарушается. Законы остаются теми же, а «пробное тело» просто движется сквозь эфир с разной скоростью, а потому и испытывает разные воздействия, которые ещё и описываются известным образом. Как я показывал в своей книге и статьях, всё это легко обсчитывается через гидродинамику. А уж после лаконичного вывода уравнений Максвелла из уравнений Навье-Стокса все вопросы должны отпасть у любого человека. Уравнения I-IV полностью соответствуют традиционным уравнениям Максвелла.

А для базовых величин типа напряжённости электрического поля, магнитной индукции, плотности тока и прочих справедливы следующие выражения:

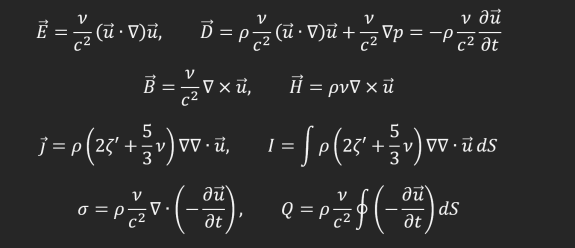
Попробуем применить преобразования Галилея к выражению для магнитной индукции:

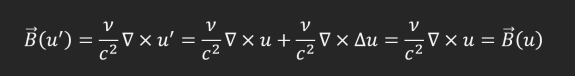
С магнитным полем всё в порядке. Но теперь применим преобразования Галилея к выражению для напряжённости электрического поля:

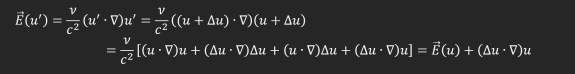
Кажется, что нарушается Галилей-инвариантность, если считать Е обычной силой, действующей на заряд. Но тут стоит вернуться к уравнениям гидродинамики.

В примере из начала статьи о столкновении двух шаров мы рассматривали изолированно два взаимодействующих объекта. Если же процесс происходит в некоторой среде, где таких взаимодействий бесчисленное множество, то даже не вполне понятно, как это рассчитывать. Но, на наше счастье, об этом уже подумали грамотные люди. Есть два подхода к анализу движения среды. Если применять лагранжев подход, то всё будет ровно как в вышеописанном примере. Мы привязываемся к конкретной частице или малому объёму среды, следя именно за ним. Тогда все выражения будут Галилей-инвариантны. Но такой подход, как правило, неудобен. Мы обычно наблюдаем за течениями жидкости, смотря в конкретную точку пространства (эйлеров подход), а не следя за какой-то отдельной молекулой воды. Поэтому помимо членов, участвующих в лагранжевом формализме и описывающих динамику конкретной частицы, будут ещё члены, описывающие пространственное распределение взаимодействий. И вот эти члены уже не будут Галилей-инвариантны, ведь они описывают динамику не конкретного механического объекта, а разницу между соседними объектами.

Это может показаться сложным (на самом деле, оно так и есть), но если просто взглянуть на формулу производной Лагранжа, которая это описывает, всё начнёт проясняться:

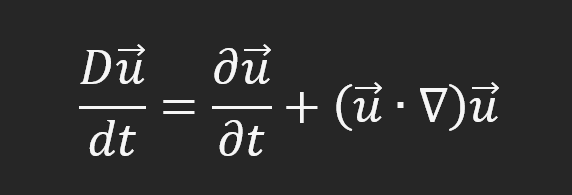
Чтобы описать действие некоторой среды на тело, обтекаемое ей, нужно вводить дополнительный член, который уж очень похож на формульное выражение для напряжённости электрического поля (E=k(u∙∇)u) в эфиродинамике. Т.е. напряжённость электрического поля в эфиродинамике описывает конкретно движение эфира относительно объекта. Если этот объект движется относительно среды с иной скоростью, то и взаимодействие будет иным. Потому нет никакого удивления, что при отказе от эфира у нас получаются всякие неразрешимые тонкости, которые называют «чисто релятивистским эффектом». Физики убрали один из объектов взаимодействия, надеясь, что всё будет в порядке. А когда стало понятно, что в порядке ничего не будет, начали выдумывать «новую физику».

Сейчас считается, что принцип относительности Галилея является частным случаем принципа относительности Эйнштейна. Но ситуация диаметрально противоположна. Подход Эйнштейна необходимо вводить лишь по той причине, что физики отказались от среды, которая и лишает происходящее физичности. Но эфир постоянно «всплывает» то тут, то там. Отсюда и тёмная материя, и тёмная энергия, и квантовая механика, и аномальные магнитные моменты. Под каждый чих вводят отдельную сущность, которая не потребовалась бы, если бы не отказались от эфира.