Физика всё-таки закончится

Буквально на днях при чтении Теории пограничного слоя Шлихтинга меня осенило. Я увидел простую формулу, которая крайне явственно показала два обстоятельства.

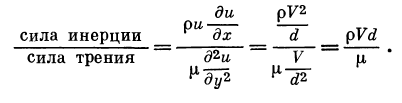
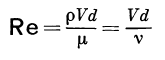
Во-первых, число Рейнольдса, которое очень часто используется при анализе обтекания тел средой, показывает отношение сил инерции к силам трения. Обычно считают, что оно показывает величину турбулентности потока, но, как говорится, есть нюанс. В знаменателе формулы для числа Рейнольдса стоит вязкость. Это значит, что чем меньше вязкость, тем выше число Рейнольдса, тем выше турбулентность среды. Предельный случай нулевой вязкости или идеальной жидкости подразумевает бесконечное значение числа Рейнольдса. Т.е. чисто логически невязкая жидкость бесконечно турбулентна. Это могло бы быть простым казусом модели, которая в предельных своих значениях не отвечает реальности, но эксперимент показывает обратное. Нередко инженеры специально делают жидкость турбулентной дополнительными препятствиями, чтобы снизить сопротивление тела среде.

На изображении можно видеть обтекание средой гладкого шара и шара с надетым на него тонким кольцом, которое закручивает жидкость, создавая вихри. Сопротивление среды резко падает. Т.е. искусственное увеличение числа Рейнольдса приближает турбулентное течение к ламинарному. И тут возникает мысль, что при огромных числах Рейнольдса вихри становятся настолько мелкими, что их влиянием на процесс можно пренебречь или рассматривать из некоторых иных соображений. Например, типичная картина для анализа влияния числа Рейнольдса на поток выглядит так:

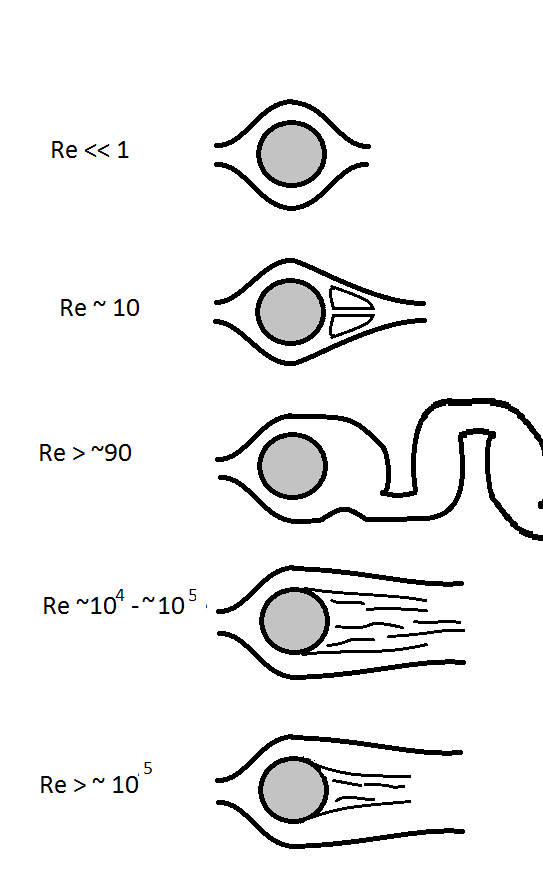
Почему-то рассмотрение обычно заканчивается на величинах в 10^6. Но весьма явно прослеживается сближение картин при минимальных и максимальных числах Рейнольдса. А ситуация между тем крайне занимательна. Если турбулентность, о которой, например, говорил Владимир Васильевич Низовцев на прошлом семинаре, высока, то все течения можно приближённо рассматривать ламинарными, т.е. нетурбулентными вовсе. Сначала течение ламинарно. По мере роста числа Рейнольдса или скорости потока при прочих равных, у нас начинают возникать неоднородности и завихрения. В некоторый момент появляются отчётливо сформированные вихри. Повышая скорость потока дальше, жидкость начинает преодолевать всё меньшее расстояние до того момента, как начнёт завихряться. Другими словами, чем выше число Рейнольдса, тема мельче получаются вихри. Вспоминая, что в рамках эфиродинамической модели любая элементарная частица – это вихрь эфира, мы понимаем, что всё это даёт нам богатую пищу для размышлений. Вероятно, минимальный для конкретного уровня организации материи вихрь – это и есть его частица. Сама эта частица, безусловно, состоит из более мелкой материи, в которой тоже возможны вихри своих масштабов. То же верно и для более крупных вихрей.

Возникает крайне занимательная идея, что в зависимости от масштаба одна и та же среда проявляет разные параметры дискретности. Т.е. на нашем масштабе частица или минимально различимый вихрь – это 10^-15 метра. Обусловлено это текущими параметрами исследуемой среды, эфира. Для галактик эта величина составляет 10^18 метра. Диапазон в 33 порядка. А значимые отклонения от ламинарности наблюдаются всего лишь в пяти порядках величин. Т.е. 28 порядков величин могут быть рассмотрены, как ламинарные течения без всякой турбулентности. И, что самое замечательное, каждые примерно 33 порядка все структуры будут повторяться. Эту оценку ещё стоит дополнительно проанализировать, но для начала результат очень неплохой.

Мы приходим к чрезвычайно выдающемуся выводу о том, что мы в деталях можем изучить всего один уровень организации материи диапазоном в 33 порядка, а все остальные уровни можно спрогнозировать с очень неплохой точностью на базе известных данных. Т.е. мы приходим к пониманию, что физика действительно может закончиться. Все те разговоры древних философов о том, что «что вверху, то и внизу», оказываются не только верными, но и невероятно полезными и пророческими. И, если рассуждать уж совсем глобально, пять порядков из тридцати трёх не играют такого уж существенного значения. При должном желании мы можем придумать, как использовать энергию ламинарных течений нужного масштаба. Нет никакой нужды закапываться в сложнейшую математику и физику конкретных порядков величин. Если не очень ясно, как использовать течения среды имеющегося диапазона размеров, можно углубиться в более мелкие масштабы или подняться на более высокие, где всё ламинарно, поддаётся точному вычислению и чрезвычайно предсказуемо.

Ну а второе обстоятельство состоит в том, что напряжение в механической интерпретации из одной из моих последних работ в соответствии с теорией пограничного слоя является силой инерции. При этом ток, как уже было известно ранее, — это силы вязкости. Тогда сопротивление – это и есть (в некоторых допущениях) число Рейнольдса. Но когда речь заходит о том, что любые конкретные масштабы не имеют никакого значения, все эти тонкости кажутся сиюминутными и неинтересными. Ведь всегда можно получить энергию из куда как более простых закономерностей. Нет нужды копаться в вязких жидкостях, с которыми мы и так справились несколько статей назад.