«Параллель Тучкова». Часть вторая, в которой следствие ведет геометрия

В предыдущей части нашего детектива мы остановились на констатации факта: простое изучение литературных источников не позволяет сделать окончательный выбор в пользу того, какую величину для главной параллели военно-топографической карты следует считать верной: 52° или 55°. Однако если некоторая величина проекции нам неизвестна, может быть есть способ ее рассчитать из имеющихся данных?

Но прежде чем приступать к обсуждению расчетов, давайте вспомним, что нам известно о проекции Бонна [1] и что нам пригодится в дальнейших рассуждениях. Дуги параллелей в этой проекции изображаются в виде концентрических окружностей. Центральный меридиан является прямой вертикальной линией, проходящей через общий для параллелей центр. Отрезки на центральном меридиане, которые отсекают параллели, проведенные через равные интервалы широт, также в точности равны друг другу (если мы рассматриваем построение на сфере) и «почти равны» [2], если мы рассматриваем сфероид. Важно, что вдоль центрального меридиана длины этих отрезков на проекции в точности равны длинам дуг самого центрального меридиана.

Остальные дуги меридианов – сложные кривые, направленные основной выпуклостью наружу от центрального меридиана, что и обусловливает красивые «сердцевидные» или «шлемовидные» общие очертания проекции. Эта выпуклость происходит от того, что в отличие от обычных конических проекций, меридианы отсекают на пересекаемых ими параллелях дуги, также в точности равные дугам параллелей на поверхности сферы или сфероида. Поэтому проекция Бонна сохраняет масштаб также и по параллелям и является равновеликой. Впрочем, именно поэтому она не сохраняет углы и, следовательно, приводит к заметному искажению форм фигур, особенно вдали от центра проекции.

В свою очередь, центр проекции – это точка пересечения главного меридиана с той окружностью, которая выбирается главной параллелью и широту которой нам и предстоит определить. Забегая немного вперед, скажу, что именно выбор главной параллели определяет общую форму проекции (от «сердцевидной» к «шлемовидной»), но подробное обсуждение этого вопроса нам сейчас не понадобится.

Общий вид одного из вариантов проекции приведен на рисунке ниже [3]:

А нам теперь пора приступить к решению задачи и, для начала, попробовать определить, что же такого мы можем измерить на карте, чтобы определить широту главной параллели.

Давайте выпишем из [4] основные формулы проекции.

ρ = R*(ctgφ(1) + φ(1) - φ)  (1)

E = R*(λ - λ(0))*cosφ/ρ  (2)

x = ρ*sinE  (3)

y = R*ctgφ(1) - ρ*cosE  (4)

Здесь φ(1) – широта главной параллели, φ – текущая широта выбранной точки, λ(0) – долгота центрального меридиана, λ – текущая долгота выбранной точки. Все эти величины берутся в радианах.

Далее, x и y – прямоугольные координаты выбранной точки, а R – радиус земной сферы. Для простоты будем вести все дальнейшие рассуждения для сферы, а не для сфероида. Как мы скоро увидим, это упрощение никак не помешает расчетам.

Рисунок из учебника В.В.Каврайского с общим построением проекции я уже приводил в предыдущей части; приведу его еще раз в увеличенном виде. Нужно только иметь в виду, что формулы у Каврайского отличаются от приведенных в [4] направлением осей x и y. Я буду в дальнейшем использовать систему [4], где ось x направлена по горизонтали, а ось y – по вертикали [5].

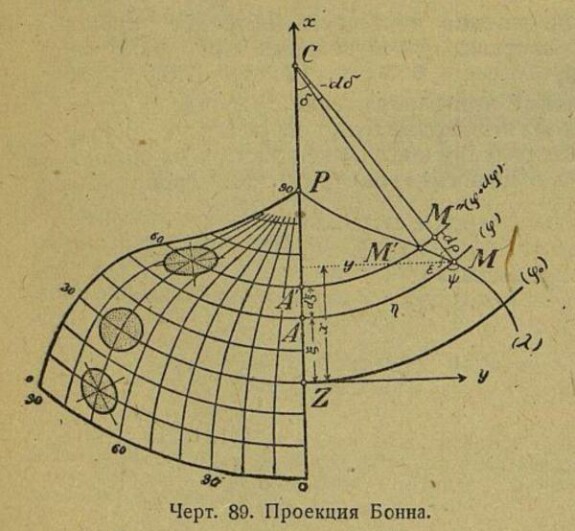
Величина ρ – это радиус окружности на проекции для выбранной широты φ. Было бы очень заманчиво использовать для определения нашей искомой главной параллели φ(1) (на рисунке Каврайского она обозначена φ(0)) эту величину ρ, поскольку она зависит только от текущей широты, широты главной параллели и наперед заданного радиуса земной сферы по формуле (1). Однако это невозможно, поскольку общий центр всех окружностей-параллелей (точка C на рисунке) лежит далеко за пределами любого листа из всего покрытия карт, и найти его простыми геометрическими построениями на листе карты вряд ли получится.

Тогда посмотрим на величину Е. У Каврайского эта величина называется δ и определяет угол ACM на рисунке выше: угол между центральным меридианом и отрезком, проведенным из общего центра C в точку на окружности (параллели), определенную выбранной величиной λ – долготы точки на местности. Тем самым, точка, определяемая широтой φ и долготой λ однозначно определяется и на проекции. Однако и здесь есть непреодолимая на первый взгляд сложность. Если направление главного меридиана мы можем определить на любом листе карты (оно попросту совпадает с вертикальными сторонами листа), то вторая сторона угла, отрезок CM, так просто не определяется. Этот отрезок не совпадает с линией меридиана PM, а отклоняется от него тем сильнее, чем дальше от центрального меридиана находится лист карты с точкой M, что хорошо видно на рисунке выше. Других же направлений, кроме линий рамки карты, окружностей-параллелей и сложных кривых-меридианов на карте нет.

Задача выглядит невыполнимой, однако не будем торопиться. Попробуем провести некоторые преобразования, включающие величину Е ( или δ – по Каврайскому).

Для простоты положим  λ(0) = 0 (как это и принимается для проекции карт-трехверсток) и возьмем производные x и y из формул (3) и (4) по λ при постоянной φ:

dx/dλ = ρ*cosE*(dE/dλ) = ρ*cosE*(R*cosφ)/ρ  (5)

dy/dλ = -ρ*(-sinE)*(dE/dλ) = ρ*sinE*(R*cosφ)/ρ (6)

Тогда

dy/dx = (dy/dλ):(dx/dλ) = sinE/cosE = tgE  (7)

Но с другой стороны, dy/dx = tgα, где α – угол наклона касательной к графику y = f(x) при φ = const в точке λ, то есть к выбранной параллели φ при данной долготе λ. Следовательно, и E имеет геометрический смысл этого угла наклона.

Перенесем теперь то, что у нас получилось и что потребуется в дальнейшем, на отдельный рисунок. Точка M на рисунке и есть та точка с выбранной широтой φ и долготой λ, в которой нам нужно теперь определить угол наклона касательной к параллели. В отличие от угла δ Каврайского мы это сможем сделать, не выходя за границы листа карты.

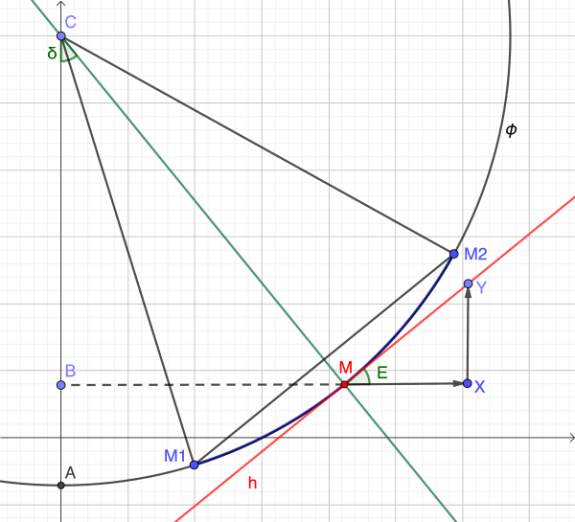
Для нахождения угла наклона этой касательной нам нет нужды стоить касательную проведением перпендикуляра h к отрезку CM, положение которого неизвестно по причинам, изложенным выше. У нас даже нет необходимости строить саму касательную h. Достаточно отложить от точки M в обе стороны две равные дуги (MM1 и MM2) и соединить их хордой. По известному свойству такая хорда будет параллельна касательной и следовательно, иметь тот же угол наклона, который и следует измерить. А можно поступить еще проще. Соединив хордой две точки пересечения параллели обозначенными на карте меридианами (скажем, те же точки M1 и M2) и зная их долготы λ1 и λ2, можно использовать угол наклона этой хорды для расчетов в точке λ, которая по построению лежит ровно на середине дуги M1M2, а по изложенному выше свойству проекции, имеет и долготу, равную среднему значению из двух крайних долгот: λ = (λ1 + λ2)/2 [6].

Теперь, имея под рукой подходящую теоретическую основу методики, я мог, наконец, заняться измерениями. Стоит сразу сказать, что в 2011 году единственной доступной мне программой, куда я мог загрузить изображение карты, сделать необходимые построения хорд и померить их углы наклона, была программа Global Mapper. О связанных с ней возможных недостатках я скажу несколько слов в конце этой части, здесь лишь коротко опишу саму методику.

После загрузки растрового файла с листом карты в программу визуально с увеличением находились точные участки пересечения меридианов с параллелью или параллелями и инструментом «Дигитайзер» строились искомые хорды. В свойствах получаемого векторного объекта можно было найти почти нужную мне информацию – с той только разницей, что Global Mapper дает сразу не необходимый угол наклона к горизонтали, а азимут – отклонение проведенной линии от направления юг-север. Поэтому нужные углы следовало бы получать вычитанием определенного таким образом азимута из 90°. Но поскольку необходимо было еще и учесть поправку на неточную «горизонтальность» растра при сканировании (небольшие повороты листов), действия можно было слегка сократить:  для каждого листа определялись еще и азимуты верхней и нижней горизонтальной рамок карты, усреднялись между собой и из полученной величины вычитался азимут хорды, при этом сразу получался наклон хорды в градусах относительно горизонтальных рамок карты (оси x [5]).

Все промежуточные действия и расчеты приведены в прилагаемой к этой части таблице Excel [7]. Данные 2011 года в ней сохранены в неизменном виде, при публикации был добавлен лишь один столбец, где были определены даты создания листов карт – они нам понадобятся.

Если мы еще раз посмотрим на формулу (2), то легко увидеть, что зависимость угла E от долготы λ при постоянной широте φ линейна. Следовательно, измерив для какой-то выбранной широты углы наклона касательной для выбранных долгот способом, описанным выше, мы можем построить модель простой линейной регрессии и найти ее параметры традиционным методом наименьших квадратов.

Тут можно сделать еще два упрощения. Во-первых, если как мы сделали ранее, положить λ(0) = 0 формула (2) функции E(λ) = aλ  + b (где a = R*cosφ/ρ) не будет содержать свободного члена b, поэтому считать достаточно только коэффициент при λ. А во-вторых, можно положить R = 1. Тогда во всех дальнейших вычислениях все величины с размерностью длины (ρ, x, y) будут получаться в «единицах R», то есть в радиусах земной сферы. Нам это никак не помешает, поскольку нас интересуют только вычисления угловых мер, а именно φ(1).

Пробные вычисления линейной регрессии были сделаны для двух параллелей: 55°40' (55,66667°, XI-й ряд карт) и 55°20' (55,33333°, XII-й ряд). На соответствующих листах файла приведены результаты статистической обработки. Даю их лишь для справок, поскольку лучшие результаты дал обсуждаемый немного ниже метод. Отмечу лишь, что для параллели 55°40' расчет дал значение для главной параллели 52,53° (отклонение в «3 сигма» равно 0,424°), а для параллели 55°20' – 51,62° («3 сигма» равно 0,483°).

99%-ный достоверный диапазон примерно в полградуса в каждую из сторон вокруг значения 52° – неплохой результат для «прикидки» метода, но хотелось результатов поточнее. Можно было бы взять весь массив измерений, но проблема в том, что формула (2) линейна по λ, но для разных параллелей мы уже имеем нелинейную зависимость от второй переменной – широты φ. Следовательно, методы линейной регрессии тут неприменимы.

К счастью, процедура для решения таких задач давно известна и широко применяется. Она заключается в подборе необходимого оптимального значения φ(1) итерационными методами. А в качестве критерия «оптимальности подбора» используется та же сумма квадратов отклонений измеренного угла E от рассчитанного на каждом шаге последовательных итераций. Задача сводится к нахождению минимума этой суммы квадратов. Эта процедура реализована и в пакете Excel и называется «Поиск решения». Задавая произвольное стартовое значение для φ(1) и указывая в настройках процедуры что нужно менять (в нашем случае – ячейку «Пробный угол») и что мы должны получить (в нашем случае – минимум суммы квадратов разности расчетного и измеренного углов) мы и получаем желаемое значение φ(1), к которому сходится алгоритм поиска [8]. Полная таблица с расчетом и приведена на первом листе прилагаемого файла.

Из таблицы видно, что всего было обработано свыше 100 точек на 63 растрах с измерениями на 4 параллелях: 52°, 55°20', 55°40' и 59°. Независимо от того, какой «пробный угол» выбирался в начале расчета (от 40 до 80°) и какой конкретный алгоритм минимизации (Ньютона или «сопряженных градиентов») использовался, процедура всегда сходилась к одному и тому же значению, близкому к 52° (51,5° при расчете по всему массиву точек).

В общем массиве были также отмечены «плохие» растры (всего 9 из 63): те, для которых отклонение измеренного угла от расчетного (хотя бы для одной точки на растре) по завершении работы алгоритма оптимизации остается больше 20' и проведены еще расчеты: без учета этих растров (в таблице они отмечены красным цветом) и только лишь по ним. Окончательный результат для оставшихся растров получился равным 51,70° («3 сигма» равно 0,42°). Что же касается «красных» растров, то отдельный расчет по ним дал величину даже меньшую, чем расчет по «хорошим» растрам: 50,78°, но, как и следовало ожидать, при существенно большей величине «3 сигма»: 1,33°.

И наконец, поскольку заметного увеличения точности расчета (по сравнению с методами линейной регрессии) добиться не удалось, был сделан вывод о том, что необходимо повысить точность самого определения углов наклона хорд на растрах и измерять угол на большей длине хорды, а не между двумя соседними меридианами. Для этого были выделены несколько листов, на которых присутствовали пересечения параллели сразу тремя меридианами и проведены построения для двух крайних меридианов (и соответственно, расчет для среднего между ними меридиана). При таких измерениях процедура оптимизации сошлась к значению 52,15° («3 сигма» равно 0,38°), что и позволило сделать окончательный для того исследования вывод: ни о какой величине в 55° для главной параллели, по крайней мере для исследованного набора листов, не идет [9].

В первой части я уже писал о том, почему мне захотелось вернуться к этому вопросу: огромный «навес авторитетного источника», сложившийся на сегодняшний день. Игнорировать его никак нельзя, напротив, всегда нужно исходить из «презумпции верности» таких источников. Поэтому, если пытаешься их опровергнуть, или поставить под сомнение, то и аргументы должны быть безупречными. А при внимательном рассмотрении тогдашних данных и расчетов оказалось, что они все же содержат ряд недостатков, которые теперь и эти данные с расчетами могут поставить под сомнение.

Обсуждение важности полученных результатов вообще я, пожалуй, отложу до следующей части нашего рассказа. Пока же ограничусь формулировкой, несколько смягченной по сравнению с формулировкой, данной мною в 2011-м году: с учетом оговорок сделанных выше, данные расчетов главной параллели проекции Бонна для военно-топографической карты по состоянию на 2011 год указывали на ее значение в 52° с вероятностью выше 99%.

1. Все же, наверное, «Бонн», как это следует из правил произношения французской фамилии (Rigobert Bonne) и как это писали в течение XVIII-XX веков люди, для которых французский язык был вторым, а то и первым разговорным. Когда Бонн превратился в Бонне? трудно сказать. Возможно, стали путать с похожей распространенной фамилией Bonnet – тот действительно, Бонне.

2. Точный смысл этого «почти» лежит вне рамок текущего обсуждения, достаточно сказать, что разница между 20-минутными интервалами параллелей (такие интервалы занимают почти целый лист карты по высоте) на самом севере всего покрытия трехверсток и на самом юге, посчитанная по уточненным «эллипсоидным» формулам, составляет всего около 80 метров, или примерно 0,6 мм в масштабе карт, что лишь ненамного превышает предельную точность масштаба карт. В пределах одного и того же листа и, соответственно, на меньших интервалах между параллелями, такая разница вообще неощутима.

3. В.В. Каврайский. Математическая картография, М.-Л., 1934, с.46

4. Map Projections – A Working Manual. U.S. Geological Survey, Washington, 1987, p. 140.

5. Здесь уместно будет напомнить, что направления осей x и y совпадают с направлениями сторон рамки любого листа карты. Это важное обстоятельство пригодится нам в дальнейшем.

6. Из построения касательной, кстати, видно, что мы могли бы даже не заниматься дифференцированием: только в том случае, если прямая h – касательная, будут равны углы δ и Е, поскольку каждый из них будет дополнять до 90° один из двух вертикальных углов, которые в свою очередь обязаны быть равными.

7. Стоит еще раз повторить, что все исходные и желаемые конечные угловые величины приводятся в градусах, но все промежуточные расчеты ведутся в радианах.

8. Здесь как раз уместно наконец пояснить, почему можно упростить вывод формул, избегая учета «эллипсоидности» земной поверхности. Дело в том, что формула для E на сфероиде отличается от формулы на сфере лишь тем, что вместо величины R в ней стоит величина a/√(1-e2sin2φ), где a – большая полуось сфероида, e – его эксцентриситет. Легко видеть, что если мы рассчитываем параметры линейной регрессии для постоянного значения φ, то и этот множитель будет постоянным, полностью аналогично R. Если же мы решаем задачу для разных φ итерационным методом, то нелинейная зависимость коэффициента от φ вообще никак не мешает расчету, поскольку на каждом шаге для каждой точки рассчитывается свой квадрат разности отклонения расчетного и измеренного значения, а величины λ и φ просто являются параметрами этого единичного вычисления.

9. В этом, кстати, легко убедиться даже до процедуры «поиска решения». Достаточно подставить в таблицах в ячейку «Пробный угол» последовательно значения в 55° и 52° и увидеть, что в первом случае сумма квадратов отклонений примерно в 30 раз превышает таковую во втором случае.