«Параллель Тучкова». Часть третья, в которой наконец-то становится понятно, почему это важно

Теперь наконец-то подошло время поговорить о том, в чем важность исследования параметров проекции Бонна для трехверстной военно-топографической карты, а именно – широты ее главной параллели. Может быть действительно, речь идет лишь о восстановлении «исторической справедливости» и, как я однажды опрометчиво написал В.Г. Щекотилову, вопрос заключается в «одном-двух пикселях хорошего скана»?

Ответ на этот вопрос, как обычно: «it depends». Или, выражаясь по-русски, «и да, и нет».

Чтобы понять, как так может быть, рассмотрим, как ведет себя проекция Бонна при разных значениях широты главной параллели для всего земного шара. На трех рисунках ниже широта главной параллели возрастает от 0° (этот частный случай проекции называют «синусоидальной») через 45° до 90° (а этот частный случай еще называют «проекцией Вернера»):

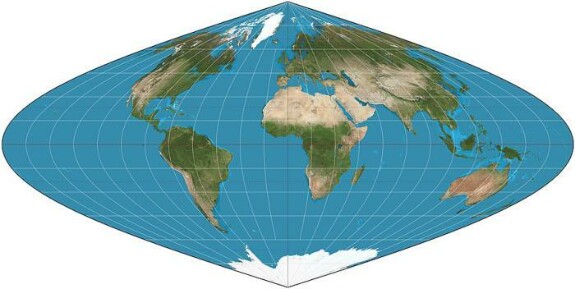
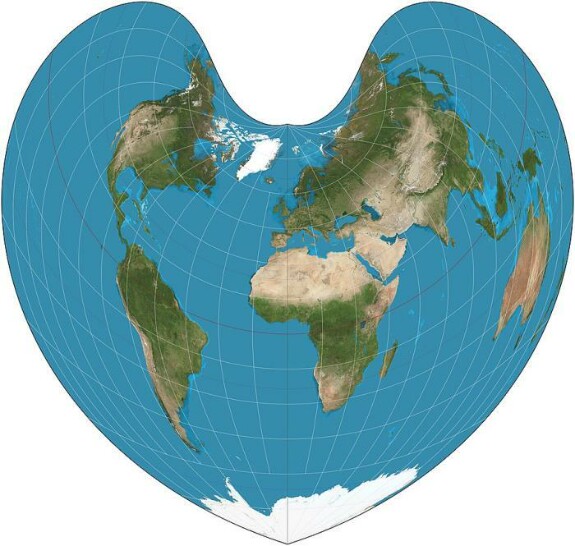
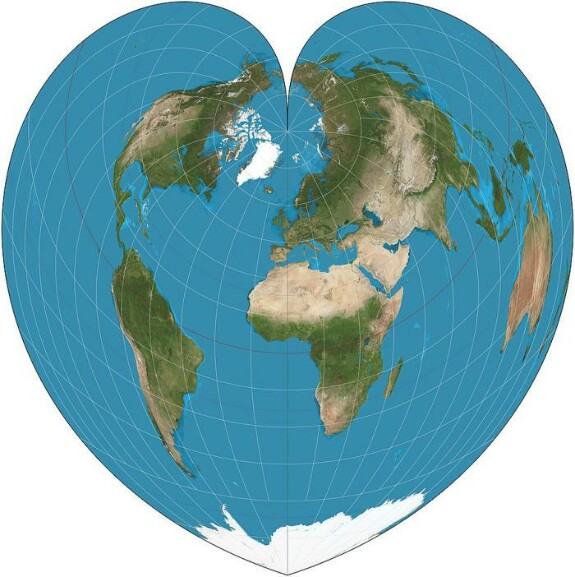
Помимо общего изменения формы проекции от «шлемовидной» до все более «сердцевидной», можно заметить, что изменяется также кривизна параллелей – от прямых линий, перпендикулярных главному меридиану при 0° до окружностей все меньшего радиуса [1].

Для исследуемых нами трехверсток проекция будет выглядеть очень похожей на средний рисунок, с той только разницей, что центральный меридиан у нее не Гринвичский, а Пулковский, и всю картинку континентов следует повернуть вдоль параллелей примерно на 30° в западном направлении.

А теперь вспомним о том, как выглядит линейная (например, верстовая или километровая) прямоугольная сетка проекции Бонна.

Основные линии сетки образованы непосредственно внутренними рамками каждого листа карты. А каждый лист представляет из себя прямоугольник шириной в 23 и высотой в 16,5 дюймов (69 на 49,5 верст «на местности»). Центральный (Пулковский) меридиан принят за 0° долготы и проходит точно между 8 и 9 вертикальными колоннами разграфки. Один из вариантов такой сетки (параллели и меридианы на нем не показаны) приведен на рисунке ниже.

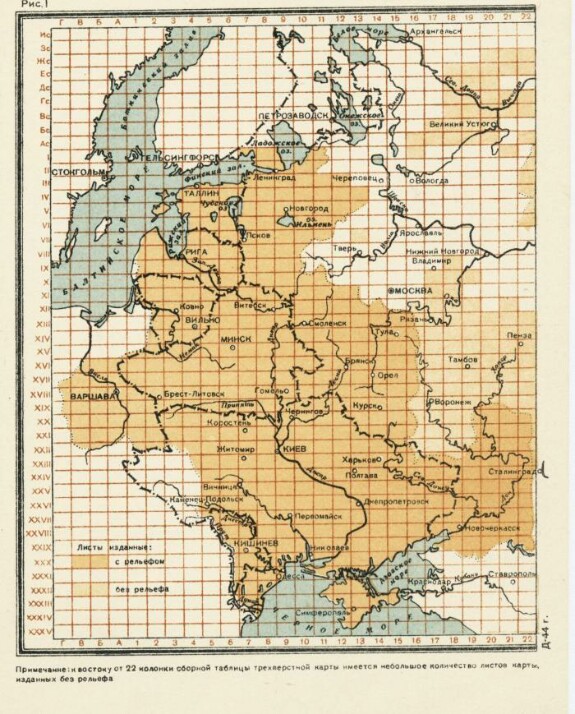
Из того, что 8 и 9 колонны жестко зафиксированы на Пулковском (центральном) меридиане следует, что и все остальные листы зафиксированы «по горизонтали».

Но точно так же сетка зафиксирована относительно центрального меридиана и «по вертикали» и никак не сдвигается при изменении широты главной параллели. Во-первых, начальная точка отсчета линейной сетки проекции Бонна всегда зафиксирована на центральном меридиане (λ(0)) и при некоторой определенной широте φ(0) [2]. А во-вторых, в проекции Бонна масштаб по центральному меридиану в точности равен 1 (а равноотстоящие друг от друга по широте параллели всегда отсекают на центральном меридиане отрезки равной длины) и поэтому все остальные линии всегда занимают одно и то же положение на центральном меридиане независимо от значения широты главной параллели.

Но если на центральном меридиане положение дуг параллелей всегда остается одним и тем же, а линейная сетка представляет собой набор жестких прямоугольников, то очевидно, что при изменении кривизны параллелей (например, увеличении кривизны при увеличении широты главной параллели, как это было показано на рисунках выше) точки пересечения параллелей с вертикальными линиями линейной сетки будут смещаться и этот эффект будет тем сильнее, чем дальше от центрального меридиана находится точка пересечения.

На словах это выглядит замечательно, но как понять количественную сторону эффекта? Для этого можно воспользоваться ранее разработанным калькулятором проекции Бонна для трехверстной карты, в котором есть специальный блок, рассчитывающий линейные координаты точек пересечения границ листов с заданными параллелями.

Такой расчет был проведен в двух вариантах: для листа, непосредственно примыкающего к центральному меридиану (лист XIX-9) и достаточно удаленного [3] от него на восток листа XIX-14. Для каждого из листов был проведен расчет ординаты точки пересечения выбранной «пробной параллели» с правой рамкой карты для разных значений главной параллели (от 52 до 55°). В качестве такой «пробной параллели» была выбрана параллель в 52°, как имеющая приблизительно среднюю кривизну в диапазоне всего покрытия карт.

Изобразим то, что мы исследуем, на рисунке. При увеличении широты главной параллели (скажем, от 52 до 55°) обозначенная стрелкой точка пересечения пробной параллели (52°) и рамки карты должна смещаться вверх за счет увеличения кривизны линии (уменьшения ее радиуса):

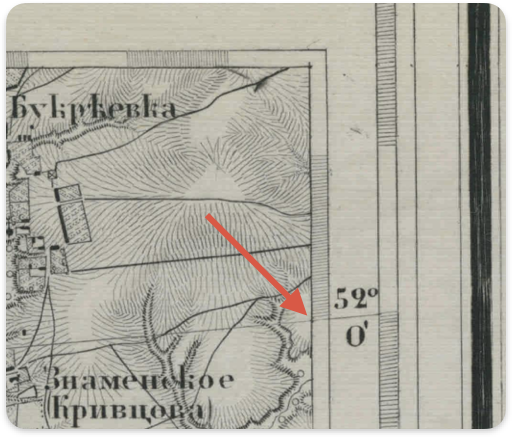
Результаты представлены в таблице ниже и в приложенном файле. Абсциссы левой и правой рамки листа обозначены соответственно XL и XR, а ординаты точек пересечения с параллелью – соответственно, YL и YR [4]. Все промежуточные расчеты в таблице традиционно проведены в английских футах, а в последней колонке изменение ординаты точки пересечения (при изменении широты главной параллели от 52 до 55°) для наглядности приведены в метрах.

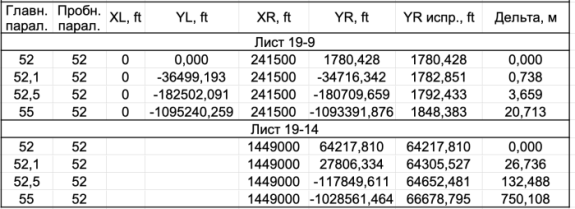
Из таблицы сразу видно, что для листа, непосредственно примыкающего к центральному меридиану максимальное изменение ординаты точки пересечения составляет около 20 метров. В масштабе карты (1:126000) это составляет примерно 0,16 мм, что даже немного меньше предельной точности масштаба карты и действительно составляет около «двух пикселей хорошего скана» в 300 dpi!

Однако совсем другая картина наблюдается для достаточно удаленного от центрального меридиана листа. Даже сравнительно небольшое (на полградуса) изменение широты главной параллели вызывает сдвиг точки пересечения в несколько раз превышающий величину предельной точности масштаба. А при изменении широты до 55° такой сдвиг достигает величины в 750 метров! Это такая величина, которая видима буквально невооруженным глазом (и примерно равна половине минутного деления на рамке).

Давайте теперь зафиксируем первый важный факт. При изменении широты главной параллели сдвиг градусной сетки относительно рамок карты практически незаметен вблизи центрального меридиана, но может составлять сотни метров на местности для листов карты, находящейся в достаточном удалении.

Таким образом, если вы используете для привязки карты не только точки пересечения градусной сетки, но и точки пересечения линий параллелей и меридианов с рамкой и при этом применяете неверное значение широты главной параллели, вы рискуете ошибиться в точности привязки на сотни метров.

Но и это не все. Даже если использовать для привязки только лишь градусную сетку (и возможно, отсчитывать широты и долготы пересечений с рамкой карты по минутным делениям рамки, а не линейными величинами x и y), вы все равно будете подвержены той же самой ошибке. Чтобы понять, почему так получается, достаточно вспомнить, что при построении карты параллели и меридианы на каждом листе проводятся как гладкие линии, соединяющие определенные рассчитанные точки, в том числе и лежащие на рамке карты. А расположение этих точек рассчитывается в линейных единицах с использованием формул проекции, и конечно же, с использованием верного значения широты главной параллели. Таким образом, каждая точка пересечения меридиана и параллели имеет верные географические координаты и x-y-координаты относительно рамок карты.

Но если при привязке вы используете неверные значения для широты главной параллели, то та же самая точка, изображающая пересечение параллели с меридианом в вашей системе координат будет иметь те же прямоугольные координаты, но совершенно другие географические. А приписав этой точке значения координат, обозначенные на карте, вы тем самым получаете погрешность привязки, которая тем больше, чем дальше от центрального меридиана находится привязываемый вами лист. И как уже было посчитано выше такая погрешность достигает многих сотен метров [5].

Итак, мы с вами выяснили, что величина самого эффекта сдвига градусной сетки относительно прямоугольной может иметь вполне заметную величину. Однако, пока еще осталось неизвестным, можно ли в принципе достаточно точно оценить влияние изменения широты главной параллели на ту величину, которую было предложено измерять в предыдущей части: наклон касательной к параллели в точке пересечения с меридианом. Как читатель запомнил из этой части, эту величину мы обозначили E:

E = R*(λ - λ(0))*cosφ/ρ,

где ρ = R*(ctgφ(1) + φ(1) - φ),

или положив λ(0) = 0 (как это сделано для центрального меридиана трехверстной карты) и после сокращения R:

E = λ*cosφ/(ctgφ(1) + φ(1) - φ)

Напомню, что φ, λ и φ(1) (широта, долгота выбранной точки и широта главной параллели соответственно) измеряются в радианах, это позволяет, в частности, складывать котангенс угла с самим углом.

В зависимости E от λ при постоянном φ нет ничего особенно интересного: это набор прямых, проходящих через точку (0,0) и имеющих угол наклона, однозначно определяемый выбранной параллелью φ и широтой главной параллели φ(1). Именно этот факт позволил в предыдущей части получить первые оценочные значения для φ(1) на ограниченном количестве измеренных углов наклона.

Гораздо интереснее выглядит зависимость E от широты φ при постоянной долготе λ (то есть, при движении «вверх-вниз» по выбранному меридиану). Не буду рассматривать поведение этой функции за пределами реального диапазона широт (хотя за этими пределами график функции и выглядит очень интересно); ограничимся диапазоном широт от 0° (экватор) до 90° (Северный полюс). Для того, чтобы рассмотреть побольше подробностей, ограничимся еще лишь положительными величинами долгот (к востоку от центрального меридиана; к западу от него кривые для E будут симметричны относительно горизонтальной оси и будут лежать в отрицательной области E). На рисунке ниже приведены 4 варианта графика. Первая пара кривых построена при фиксированной долготе в 11° [6] и широте главной параллели в 55° (синяя кривая) и 52° (оранжевая кривая). Вторая пара – при фиксированной долготе в 2° (вторая по счету колонна разграфки от центрального меридиана) и так же для широты главной параллели в 55° (зеленая кривая) и 52° (фиолетовая кривая). Для удобства восприятия все шкалы углов также пересчитаны из радианов в привычные градусы.

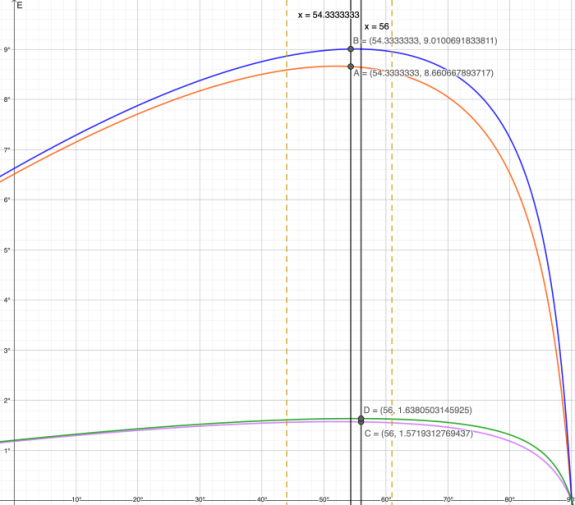
Первое, что бросается в глаза – это то, что при движении от экватора (0° широты) вдоль кривой (то есть, вдоль выбранного меридиана) величина E вначале нарастает в полном соответствии с предыдущим рассмотрением (уменьшается радиус окружности-параллели, следовательно увеличивается угол наклона касательной к ней). Однако в дальнейшем кривая проходит через максимум [7] после чего ближе к полюсу резко идет вниз, в нулевую точку. Это происходит из-за того, что в полярной зоне все меридианы идут все ближе и ближе к центральному меридиану (где наклон касательной равен нулю) и этот эффект перекрывает увеличение кривизны параллели на данном меридиане.

Второе – это то, что для диапазона широт всего покрытия карт-трехверсток (на рисунке он отмечен желтыми пунктирными линиями) разница в величинах E для кривых с разной широтой главной параллели почти максимальна (по крайней мере, для меридианов близких к восточному и западному краям покрытия). Следовательно, у нас есть шанс различить эти величины, измеряя их на реальных картах.

Давайте тогда и рассмотрим реальные примеры.

Возьмем на пробу два листа трехверстной карты: лист X-10, содержащий точку пересечения меридиана 2° с параллелью 56° и лист XIII-18, содержащий точку пересечения меридиана 11° с параллелью 54°20'. На рисунке выше этим точкам пересечения на картах будут соответствовать точки пересечения цветных кривых и вертикальных прямых, обозначенных черным цветом. Листу XIII-18 соответствуют точки A и B (для широты главной параллели в 52 и 55° соответственно), а листу X-10 – точки C и D. Ординаты всех этих точек пересечения можно найти графическим методом; численно они будут равны рассчитанным углам наклона касательной в точке пересечения параллели и меридиана к горизонтальной рамке карты.

Давайте теперь измерим эти углы на листах. Новую методику такого измерения я изложу в следующей части, здесь лишь приведу конечные данные. Для меридиана 11° (верхняя пара кривых) величина такого наклона получилась равной 8,77°, а для меридиана в 2° – равной 1,55°.

Теперь я забегу немного вперед и сообщу, что среднеквадратичная ошибка (отклонение измеренных углов от расчетных) на массиве из около 100 измерений оказалась равной примерно 5 минутам (0,08 градуса). На первый взгляд отклонение в 0,11° для точки A (8,77° - 8,66°) выглядит великоватым, однако мы тут же вспоминаем, что примерно треть точек должна иметь отклонения, превышающие одно такое «стандартное отклонение» [8]. В то же время, отклонение от рассчитанной величины в точке B составляет уже 0,24°, что составляет примерно 3 стандартных отклонения. Снова вспомнив о том, что вероятность таких или больших отклонений должна быть 1% или меньше, делаем вполне уверенный вывод о том, что наша экспериментальная точка намного более вероятно принадлежит красной расчетной кривой (главная параллель при 52°), нежели чем синей (главная параллель при 55°).

В то же время для меридиана 2°, близкого к центральному меридиану, такого вывода сделать нельзя. Разница в величинах ординат для расчетных точек C и D равна всего-навсего 0,06° и наша экспериментальная точка лежит в пределах одной среднеквадратичной ошибки от обеих кривых (там, где должны лежать примерно две трети экспериментальных точек). Однако это не значит, что измерения в этой области бесполезны: как мы с вами увидим в дальнейшем, эти измерения помогут в статистической обработке всего массива измерений. Пока же можно сказать, что данные в этой области не помогают в случае единичных измерений.

Теперь можно зафиксировать второй важный вывод. Предлагаемый метод определения параметра проекции путем прямого измерения наклона касательной к параллели позволяет сделать выбор между величинами этого параметра даже в случае единичных измерений (если мы проводим эти измерения достаточно далеко от центрального меридиана), причем простым и доступным способом. Во всех остальных случаях, как я покажу в дальнейшем, нам поможет статистическая обработка данных [9].

И наконец, третий по порядку, но не по значимости вывод. Как мы уже видели из предыдущей части (а в этой части получили и дополнительные данные), любые утверждения в литературе, относящиеся к параметрам проекций, следует проверять и желательно подкреплять или опровергать дополнительными вычислениями, невзирая на авторитетность авторов этих утверждений.

Примечания.

1. Чем меньше радиус окружности, тем больше ее кривизна. Прямая линия – это окружность с бесконечно большим радиусом.

2. Эта широта φ(0) может совпадать, а может и не совпадать с широтой φ(1) главной параллели. Эти величины в общем виде полностью независимы.

3. Удаление составит ровно 345 верст, если его считать вдоль горизонтальной рамки карты.

4. Нужно только иметь в виду, что когда создавался калькулятор, задачи раздельного учета широты главной параллели φ(1) и начальной точки прямоугольной системы координат φ(0) не стояло. Поэтому в нем для упрощения всегда полагается, что начальная точка совпадает с главной параллелью: φ(0)=φ(1). Так что, если читатель захочет самостоятельно повторить расчет для других листов карты, он должен принять во внимание то, что при изменении широты главной параллели в калькуляторе вся сетка листов как целое сдвигается вместе с главной параллелью на величину YL. На эту величину в предпоследней колонке таблицы вводится поправка и получаются «исправленные» значения YR.

5. Тут уместно будет пояснить, что во всех рассуждениях выше я для упрощения рассматривал прямоугольную сетку листов карты как отдельную сущность, никак не изменяемую при деформации карты при изменении широты главной параллели и лишь только «наброшенную» на нее сверху. Совсем по-другому выглядели бы наши манипуляции, если бы (как оно и имеет место в действительности) прямоугольная сетка была нарисована на карте. Тогда при изменении широты главной параллели она бы изогнулась следом за изменением изгиба параллелей и стала бы отличаться от рассматриваемой «отдельной сущности». Собственно, именно в этом и проявляются искажения проекции (расстояний и углов) по отношению к сфероиду, а следовательно, и взаимные искажения проекций с разными параметрами. Подробное аналитическое рассмотрение вопроса здесь неуместно, вдумчивого читателя я отошлю к неоднократно цитированной в предыдущей части монографии В.В. Каврайского, где вопрос искажений рассмотрен более чем подробно.

6. Как вы уже наверное запомнили, за нуль долготы принят Пулковский меридиан, так что 11° в.д. соответствует самым восточным листам всего покрытия трехверстной карты.

7. Можно легко показать, что максимум кривой лежит в точности при широте, равной широте главной параллели. Нам этот факт пока не понадобится, поэтому более подробно на нем останавливаться здесь не будем.

8. В том случае, если отклонения (ошибки) имеют нормальное распределение. Подробнее этот вопрос обсудим позже, пока примем нормальное распределение на веру.

9. Статистически, точки вблизи центрального меридиана не «хороши» и не «плохи». Можно сказать, что они одинаково хорошо подходят для любого уравнения регрессии, которое «опирается» на дальние от ЦМ точки, в общей совокупности лишь уточняя расчетный результат.