Как работает WAVESHAPER

Формально, этот, практически всегда цифровой, метод преобразования сигналов относится к «эффектам» (как в Korg opsix и Modal) или «модификаторам» (у Modal Argon 8 есть и такое). Однако сила и разнообразие воздействий на входной сигнал у преобразователей данного типа таковы, что не будет большой ошибкой воспринимать их как самостоятельный метод синтеза сигналов наряду с FM-синтезом. Что, кстати, и стало одним из столпов легендарности непревзойдённого цифрового синтезатора Buchla 700.

Между тем, в отличие от FM, Waveshaper работает очень просто и понятно — без тени высшей математики. Достаточно будет лишь произнести фразу «Передаточная функция» (она же - «Трансфер-функция») и вот вам уже ясно, что делает с входным сигналом этот самый Waveshaper.

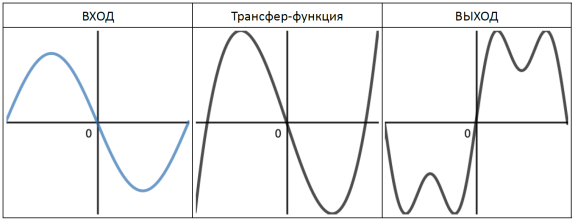
Если же вы ранее не сталкивались с понятием «Передаточной функции», то я вам предлагаю взглянуть на следующий рисунок:

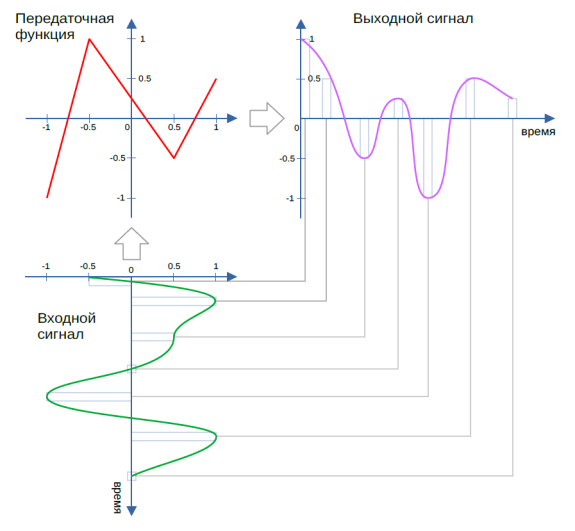
Рассматривать его нужно «снизу вверх и направо» - согласно маршруту сигнала в типичном блоке Waveshaper.

Входной сигнал на этом рисунке представлен некой произвольной волноформой, которая отображается на графике входного сигнала (внизу слева) в виде зелёной линии. Несмотря на непрерывный характер кривой, рассматривать её мы будем исключительно как дискретный сигнал, некоторые отсчёты которого отмечены на графиках бледными столбиками.

Итак, каждый отсчёт оцифрованного сигнала последовательно передаётся в некую трансфер-функцию, представленную графически в виде ломаной красной линии.

Если говорить на языке математики, то значение каждого отсчёта входного сигнала просто передаётся в (трансфер-) функцию в виде аргумента. Соответственно, каждое (вычисленное) значение функции становится (новым) цифровым отсчётом выходного сигнала, который на вышеприведённом рисунке показан линией лилового цвета.

Собственно, всё. На этом можно и закончить описание принципа работы передаточной функции.

Но если вам этого описания недостаточно, то можно просто посчитать всё вручную:

Для начал посмотрите на график входного сигнала и найдите на нём нулевой отсчёт — столбик, прямо на оси Y, с которого зелёная линия берёт своё начало. Видите какое значение у данного отсчёта?

-0.5

А вот теперь пришло время заметить, что график исходного сигнала неспроста повёрнут на 90 градусов. Сделано это для того, чтобы наглядно показать ключевой момент преобразования — проекцию значений дискретных отсчётов входного сигнала на ось X графика передаточной функции.

Собственно, сейчас мы с вами как раз и будем вычислять значение функции графически. Для этого отмечаем -0.5 на оси X передаточной функции, мысленно проводим от этой отметки вертикальный перпендикуляр до его пересечения с красной линией графика передаточной функции и, повернувшись на 90 градусов, ведём перпендикуляр уже до его пересечения с осью Y графика передаточной функции.

Не знаю как у вас, а у меня получилось значение +1. Вот мы с вами и вычислили (графически) значение (трансфер-) функции при заданном аргументе. То есть, передали ей значение аргумента -0.5, а получили +1. Вот в этом, собственно, и есть вся «магия» преобразований Waveshaperа.

Теперь отметим вот это совершенно другое относительно исходного, значение нулевого цифрового отсчёта на графике выходного сигнала и займёмся следующим цифровым отсчётом входного сигнала.

Кстати, для простоты восприятия, «одномоментные1 отсчёты» графиков входного и выходного сигналов соединены прямыми серыми линиями.

Теперь давайте выберем ещё один (следующий по времени) отсчёт на графике входного сигнала, также отмеченный столбиком. Его значение равно +1.

Откладываем +1 на оси X трансфер-функции и находим на оси Y значение функции, соответствующее такому значению аргумента. У меня вышло +0.5.

Отмечаем полученное значение такого же по времени отсчёта на графике выходного сигнала и далее повторяем вышеизложенную последовательность действий для всех отсчётов входного сигнала.

Что получилось — видно невооружённым глазом. Форма выходного сигнала радикально отличается от формы входного сигнала. И сделал всё это — Waveshaper.

Ну а теперь давайте понаблюдаем за работой Waveshaperа (и вообще трансфер-функций) на нескольких примерах (для всех этих примеров входной сигнал будет представлен простой синусоидальной формой волны).

Пример 1: Простейшая из передаточных функций — линейная функция. Она пропускает входной сигнал без каких-либо изменений

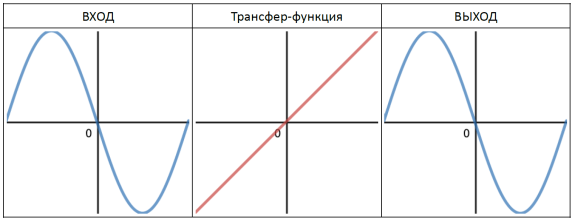
Пример 2: Воздействие простейшей из передаточных функций (линейной функции) на синусоидальный сигнал неполной амплитуды

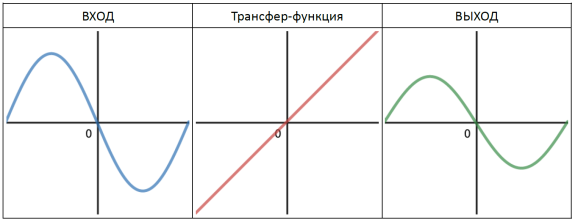
Как видите, если амплитуда входного сигнала уменьшается, то уменьшается и амплитуда выходного сигнала.

Пример 3: Передаточная функция — третий многочлен первого рода Чебышёва (гуманитарии, не спешите пугаться! К самому понятию передаточной функции это никакого отношения не имеет)

Совершенно очевидно, что сложная передаточная функция даёт более сложный результат. В этом примере трансфер-функцией является третий полином Чебышёва. Выходной сигнал, пропущенный через такой Waveshaper представляет собой синусоиду, с частотой, в три раза превышающей частоту входного сигнала, известную как «третья гармоника».

Подробное обсуждение многочленов Пафнутия Львовича Чебышёва, одного из величайших математиков XIX века, выходит за рамки данной статьи. Однако крайне полезным будет запомнить, что N-й полином Чебышёва преобразует синусоиду полной амплитуды в N-ю гармонику этой синусоиды.

Пример 4: Влияние третьего многочлена Чебышёва на синусоидальный сигнал очень малой амплитуды

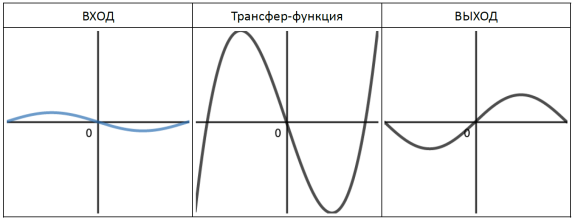
Во втором примере мы уже отмечали, что уменьшение амплитуды входного для передаточной функции сигнала, не всегда таким же образом воздействует на амплитуду выходного сигнала. Тут мы по прежнему используем третий полином Чебышёва в качестве передаточной функции, однако амплитуда входной синусоиды здесь уменьшена до 10% от исходного значения. И, как видите, выходной сигнал также является синусоидой, но уже с амплитудой, превышающей амплитуду входного сигнала.

И опять отмечаем закономерность: N-й многочлен Чебышёва преобразует синусоиду низкой амплитуды в синусоиду с такой же частотой увеличенной амплитуды.

Пример 5: Влияние третьего многочлена Чебышёва на синусоидальный сигнал условно средней амплитуды

В примере 4 было показано, что сильное уменьшение амплитуды входного сигнала приводит к похожему уменьшению амплитуды выходного сигнала. Текущий пример же гораздо интересней. Трансфер-функция в нём — всё тот же третий многочлен Чебышёва, а вот входной сигнал представляет собой синусоиду, с амплитудой, составляющей 75% от единичной. Но в отличие от всех предыдущих примеров, выходной сигнал тут уже на исходный совершенно не похож. Он имеет большую амплитуду и содержит больше гармоник, что очевидно, ведь кривая, описывающая форму выходного сигнала искривлена гораздо более замысловато.

Фактически, гармонический состав выходного сигнала представляет из себя определённую сумму первой и второй гармоник входной синусоиды.

Вышеописанную закономерность можно выразить следующим образом: N-й полином Чебышёва преобразует синусоиду «средней амплитуды» в некоторую комбинацию гармоник входного сигнала вплоть до гармоники N, но не включая её.

ИТОГ (Waveshaper с третьим полиномом Чебышёва в качестве трансфер- функции):

1. Небольшой по амплитуде сигнал Waveshaper приводит к выходному сигналу с небольшим числом гармоник.

2. Входной сигнал большой амплитуды Waveshaper приводит к выходному с гармоническим содержанием, соответствующим таковому у входного.

3. Входной сигнал с амплитудой, находящейся между условно низкими и высокими значениями, Waveshaper приводит к обогащению гармониками более высокого порядка.

Сейчас, когда вы хорошо себе представляете возможности Waveshaperа, будет наиболее уместным взглянуть на тот арсенал трансфер-функций, который перекочевал в Korg opsix из музыкальной рабочей станции Korg «01/W», выпущенной в 1991 году.

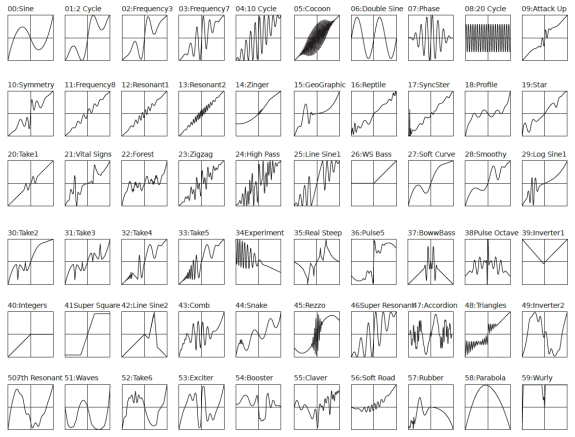
Впечатляет, не так ли?

Уверен, влиянию на звук каждой из шестидесяти вышеприведённых передаточных функций можно посвятить отдельную статью. Но это уже будет совсем другая история.

При подготовке данной статьи были использованы материалы из РЭ ID700 — гибридного программного FM/Waveshaping синтезатора, созданного по мотивам легендарного Buchla 700.