Солнце в аварийной навигации

Долготу в наших условиях можно определить по Солнцу и это довольно просто.

Хочу добавить, что мы ведь могли оказаться и в южном полушарии, или вблизи экватора. Там классно. Но Полярной там нет. В этих условиях проще всего использовать Солнце и для определения широты и долготы.

Итак - определяемся по полуденному Солнцу, разберемся сначала с долготой.

Для того, чтобы выяснить, на каком меридиане мы оказались, нужно определить время местного полудня. Сделать это можно несколькими путями, самый понятный - отметить время восхода, когда верхний край Солнца появляется над горизонтом и время захода, когда последний краешек уходит за горизонт. Из инструментария нужны только часы. Точное время солнечного полудня находится ровно между ними.

Этот способ - не самый практичный, нам придется пересекать весь наш остров для наблюдений, нам придется встречать рассвет и провожать закат. Мало того, солнце на горизонте часто бывает закрыто облачностью, или соседним островом. Но, по крайней мере эти трудности решаемы простыми средствами, например, можно использовать камал и фиксировать утреннее и вечернее время, когда Солнце находится на равных небольших высотах над горизонтом, и способ в целом, вполне рабочий.

Если уж нам разрешили секстан, практичней использовать метод Вилсона, который мы уже разбирали раньше. Здесь мы будем использовать секстан в двух сериях наблюдений, до и после кульминации Солнца. В любом случае, в результате мы получим время местного полудня - LAN, данные берем из нашего ролика, время точки пересечения восходящей (AB) и нисходящей (CD)ветки измерений. Каждая клетка графика по горизонтальной оси - 10 секунд, время (сразу отнимем 10 часов, чтобы было гринвичское) UTC 2:31:18 и 3:29:18. Складываем часы и минуты и делим на два - получается 3 часа 00 минут. И, как мы видим на графике - еще примерно 18 секунд. Это время местного полудня, выраженное временем UTC.

Специально замечу - если мы встретим рассвет и проводим закат, и проведем те же арифметические операции, мы получим те же цифры, ну, может быть секунды будут другими. Что теперь можно с этим сделать?

Мы видим, что время местного полудня на нашем острове наступает, когда в Гринвиче глубокая ночь, Солнце к ним еще не пришло, и им до полудня еще ждать 12ч00м00с - 3ч00м18с = 

11ч59м60с - 3ч00м18с = 8ч59м42с. Так как за час Солнце сдвигается по небу на 15 градусов, то за минуту - на 15 угловых минут, за секунду - 0,25 угловой минуты. Угол между нашим солнечным полуднем, и солнечным полуднем Гринвича = 120+14=134 градуса и 45+10,5=55,5 минут, причем у нас день наступает раньше, значит долгота восточная. Все просто.

Солнечный полдень не всегда наступает ровно в 12 часов местного времени. Солнце в течение года может отставать, до 14 минут, может и забегать вперед, вплоть до 16 минут времени. Каждый год картинка повторяется.

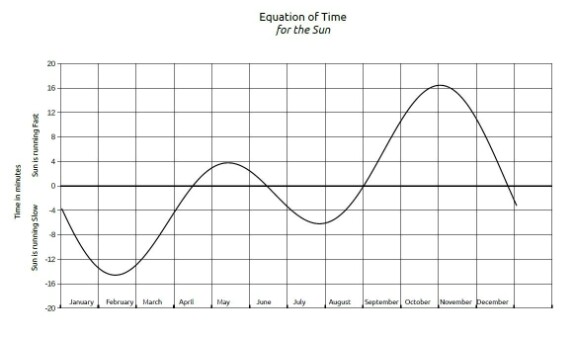
Эту поправку - уравнение времени на конкретную дату, нужно каким-то способом учесть, иначе ошибка расчета долготы может стать значительной. Размеры ошибки можно прикинуть, за минуту времени Солнце сдвигается по небу на четверть градуса - 15 угловых минут, а за 10 неучтенных минут времени мы получим ошибку определения долготы в 2,5 градуса. На экваторе - это 150 морских миль, в умеренных широтах больше сотни - многовато будет.

Для того, чтобы воспроизвести эту поправку дедовским самопальным способом, нужно запомнить две ключевые даты - 14 февраля, когда поправка составляет  (-14 минут).

Есть старое правило для запоминания - В день Святого Валентина 14 февраля, девушка опаздывает на 14 минут.

Вторая дата тоже вполне запоминаемая - Хелувин - 31 октября (+16 минут). В этот день Солнце приходит на меридиан Гринвича (линию Север-Юг)  за 16 минут до 12 часов.

Две других точки перегиба вторичны и привязаны к основным. Они как бы симметричны, и легко запоминаются.

Через три месяца после 14 февраля - 14 мая +4 минуты

За три месяца до 31 октября - 31 июля -6 минут

На точках перегиба считаем, что в течение двух недель до и после даты величина поправки не меняется.

График строится по памяти, и на график наносится точка даты, поправка на которую нас интересует.

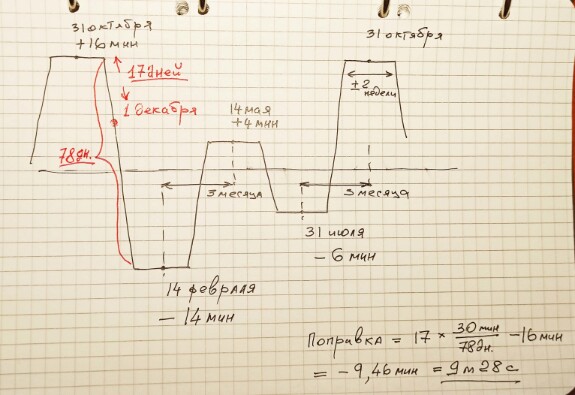
Давайте прикинем поправку на 1 декабря по нашему упрощенному графику.

Нас интересует ветка графика между 31 октября и 14 февраля. В соответствии с картинкой, с 14 ноября (31 окт + 14 дней) до 31 января (14 февраля - 14 дней) = 78 дней, и за это время поправка меняется на 30 минут (14+16 = 30). Если разделить 30 минут на 78 дней, мы получим величину изменения поправки в день. Другими словами - это скорость изменения поправки в день. От 14 ноября до 1 декабря  30 - 14 + 1 = 17 дней.  Умножаем на скорость изменения поправки в день, и отнимаем от 16 минут (поправки на дату 14 ноября). Получаем 9, 46, или, переведя десятые в секунды - 9 минут 28 секунд. 

То есть, 1 декабря Солнце приходит в нулевой меридиан раньше 12 часов Гринвича на 9 минут 28 секунд. А мы выше считали "в идеале", что в 12.

Это означает, что нашу рассчитанную выше разницу времени нужно уменьшить на эту поправку.

То есть, уточненная "самодельной" поправкой долгота будет = 120+12=132градуса 30'+(0,25 x 14c) = 132градуса 34минуты.

Давайте проверим, какую поправку мы брали с альманаха на эту дату - 10 минут 48 секунд, ошибка, вызванная неточностью расчета поправки составит 1 минуту 20 секунд, или 15' + 0,25' x 20 = 20' долготы, то есть точно меньше 20 миль, это уже кое-что.

Осталось разобраться с "аварийным" определением широты по полуденному Солнцу, и закроем, наконец, эту тему постапокалипсиса.

Что нам придется вспомнить в первую очередь, это волшебную последовательность цифр - 2..3..4. 23,4 градуса - величина наклона земной оси от вертикали, которая определяет смену сезонов в течение года. Если точнее - 23 градуса 26 минут, просто 234 запоминается навсегда и сразу.

С точки зрения наблюдателя, который смотрит на юг в северном полушарии, Солнце в течение дня описывает по небу дугу, набирая максимальную высоту в местный полдень. В этот момент Солнце находится точно на местном меридиане, наблюдатель видит его точно на географическом юге - S. 
(Все, что здесь написано, справедливо и для южного полушария, нужно просто "отзеркалить" описание. Можете заняться в качестве домашней работы.)

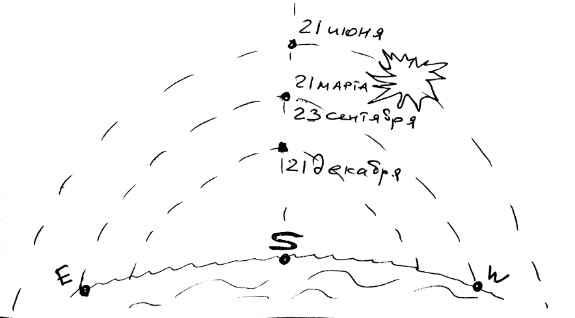
В течение года эта дуга будет в точности сохранять свою форму, сдвигаясь при этом вверх и набирая максимальную высоту в день летнего солнцестояния — 21 июня. Минимальная высота солнца в полдень будет в день зимнего солнестояния — 21 декабря.

Ровно между ними находится траектория дней равноденствия, 21 марта и 23 сентября, когда солнце восходит из-за горизонта на географическом востоке (E) и заходит точно на западе (W).

Если измерить в полдень равноденствия высоту солнца и отнять полученное значение от 90°, (это понятие называется зенитным расстоянием) без дополнительных вычислений мы получим широту места.

Дни солнцестояний тоже подходят — нужно просто добавить или отнять от результата волшебное число — 23,4°. То самое значение угла наклона земной оси, которое мы уже запомнили выше. В любой другой день, к сожалению, так просто не получится, придется вводить поправку — склонение Cолнца δ, которое принимает значения в течение года от -23,4° до +23,4°.

Для определения широты места нам нужно измерить высоту Солнца ( H ) в местный полдень, и вычислить величину склонения Солнца на эту дату (δ).

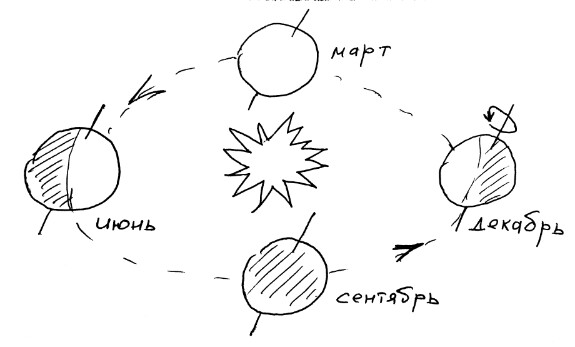
На схеме изображены Солнце и орбита Земли. Если принять для простоты, что орбита круговая, и Земля движется по орбите равномерно, то промежуточные значения склонения можно получить простым расчетом, используя только знание дат этих четырех точек, величины наклона оси вращения Земли, и способность воспроизвести годовой календарь.

  Нам нужно вычислить склонение Солнца на 1 декабря 2020 (дата наших наблюдений полуденного Солнца в видеоролике Секстан и метод Вилсона ), чтобы сравнить с табличными.  

Возвращаемся к календарю, который мы нарисовали и считаем дни

ближайшее равноденствие 23 сентября - день 266 (склонение =0°)

ближайшее солнцестояние 21 декабря - день 355 - зимнее, так что наше склонение южное - минусовое. (-23,4°)

Вспоминаем умножение и деление в столбик.

1. Вычисляем угол Альфа = 20/(20+69) * 90° = 20,2°

2. Достаем наши самоделки - транспортир и линейку, строим угол, строим прямоугольный треугольник,

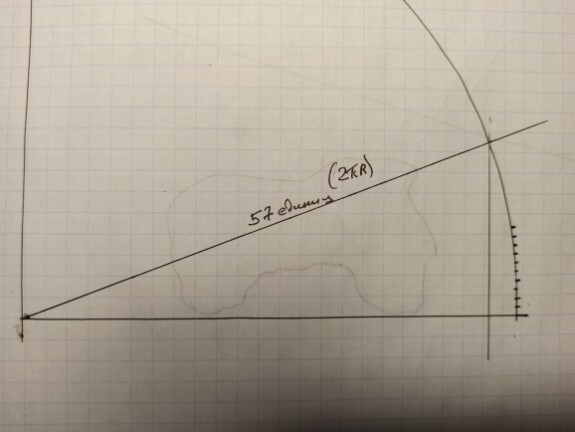
и находим результат деления прилежащего катета на гипотенузу - X / R, это будет cos Альфа. Умножаем его на наши 23,4, получаем результат 21,95. Или 21°57'.

Наше построение было в "минусовой" четверти склонения, поэтому склонение со знаком "минус", или южное.

Взятое с альманаха склонение солнца для 3 часов Гринвича - S 21°51.2' -

Ошибка наших "самодельных" эфемерид по сравнению с "настоящими" - 5,8 угловых минут, меньше 6 миль по широте.

Как видно из результатов, мы смогли определиться с помощью мореходной астрономии с довольно приличной точностью в незнакомом месте на планете Земля без альманаха.

Если у нас есть секстан и точные часы, мы попадем в область с неопределенностью по широте в 10-15 миль, по долготе - 20-30 морских миль.

Если секстана нет, и мы используем что-то самодельное для измерения высот светил, неопределенность по широте вырастет, и может составить 30-100 морских миль, а если нет и часов, то с долготой - принципиальная беда, придется решать, как жить дальше, имея определенность только с широтой места.

=================