Line Reflection
Описание
Даны n точек на двумерной плоскости, найдите, существует ли такая прямая, параллельная оси y, которая симметрично отражает данные точки, другими словами, ответьте, существует ли такая прямая, что после отражения всех точек через данную прямую множество исходных точек совпадает с множеством отраженных.
Обратите внимание, что могут существовать повторяющиеся точки.
Решение
Для лучшего понимания задачи стоит посмотреть на примеры
Пример 1:
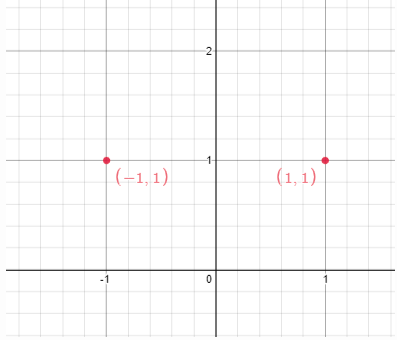
Точки (-1, 1) и (1, 1). Ответ True , т.к можно выбрать прямую x=0
Пример2
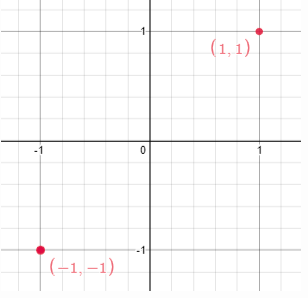
Точки (-1,-1) и (1,1). Ответ False , т.к для данных точек нельзя подобрать отражающую прямую параллельную оси y
Начнем разбираться с решением задачи.
Во первых у нас есть всего один вариант отражения, а именно отражать относительно какой-то прямой параллельно оси OY.
Что значит отразить точку (x,y) относительно какой-то прямой параллельной OY?
Любая прямая параллельная OY характеризуется значением x. Т.е мы фиксируем х, а y принимает всевозможные значения. Как например на примере снизу. Есть две прямые параллельные оси OY, которые однозначно характеризуются значением х

Таким образом точка (x,y) после отражения преобразится в точку (x1,y1). Но так как мы отражаем относительно прямой параллельно OY , то координата y не поменяется.
В итоге отраженная точка будет иметь координаты (x1,y)
Как же теперь определить есть ли такая прямая, которая отражает данное множество в себя же. Тут важно сделать следующее замечание, которое на самом деле является тривиальным.
Такая прямая и существует ТОЛЬКО тогда когда самая крайняя левая точка отражается в самую правую крайнюю точку. Действительно если самая крайняя левая точка не отражается в самую правую, а в другую. То для самой правой не найдет точки из множества, в которую она бы могла отразиться. На примере ниже если и такая прямая существует, то красная(самая крайняя левая) точка должно отражаться в синюю(самая крайняя правая)
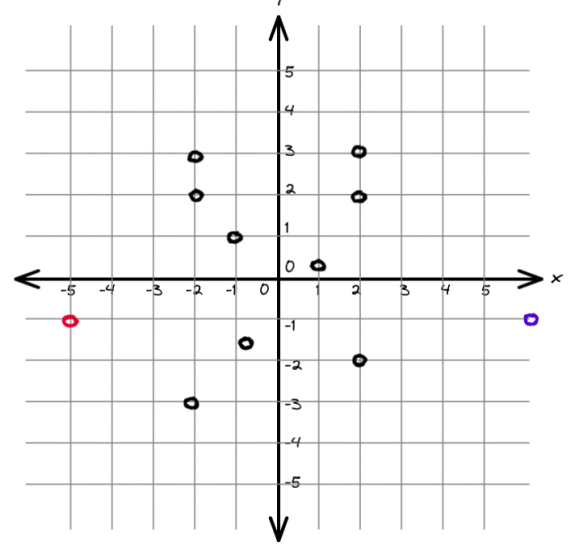
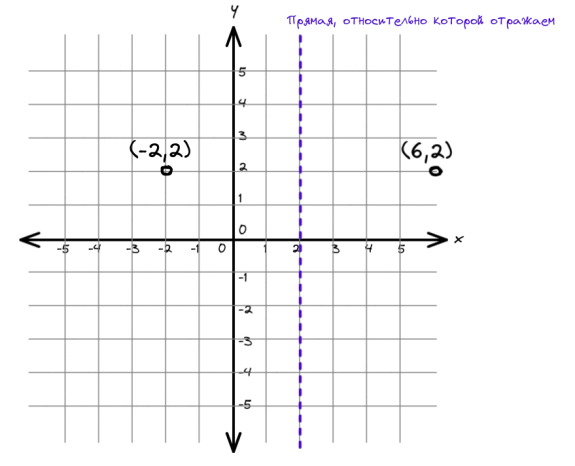
Теперь зная два факта: 1) самая левая точка(left_x) отражается в самую правую(right_x) 2) любая возможная прямая характеризуется значением Х , мы можем сказать , что единственным кандидатом для такая прямой является прямая Х = (left_x + right_x) / 2
На примере ниже такая прямая-кандидат имеет координату x = 0.5, так как самая левая точка имеет координаты (-5,-1) , а самая правая (6,-1).

Тут возникает сложность в том, что хоть и координаты точек по условию целые числа, но координата прямой может быть не целой. Как с этим бороться?
Давайте посмотрим как мы получаем координату отражаемой точки

Т.е мы видим, что расчет координаты X для отраженной точки всегда одинаков. Что более важно, мы всегда умножаем значение координаты прямой на два. Поэтому нет смысла делить выражение (left_x + right_x) на два, так как мы всегда после этого умножаем значение прямой на два. Т.е решение проблемы с вещественной координатой следующее: будем хранить не координату прямой, а удвоенной значение координаты.
Теперь зная единственно возможного кандидата нужно проверить отражает ли данная прямая исходное множество в себя же.
Это можно сделать следующим образом : создадим хэш-мапу где ключом будет является координаты точки (x,y) , а значением количество таких точек. Вспоминая условие задачи у нас могут быть повторяющиеся точки.
Далее нам нужно пройтись по данной хэш-мапе, для каждого ключа определить точку в которую она отразится относительно нашего кандидата. Если отраженной точки нет в хэш мапе или же значение в отраженной точке не равно значению в отражаемой , то кандидат не подошел. И ответ False
Если же мы прошли по всем точкам и для всех кандидат подошел, то ответ True
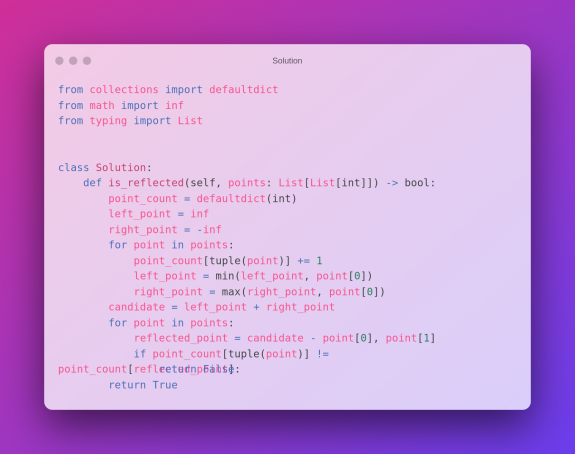
Пример решения Python
leetcode
medium
math




