О решение алгоритмических задач
Решение алгоритмических задач — это не только проверка умения программировать, но и способность мыслить логически, анализировать и оптимизировать процессы. При решении задач важно учитывать не только корректность алгоритма, но и его эффективность, включая время выполнения и использование памяти.
Понимание задачи и выбор подхода
Первый шаг — тщательный анализ задачи. Важно полностью понять, что от вас требуется, определить входные и выходные данные, ограничения и специальные условия. После понимания задачи выберите подход к её решению. Это может быть прямое решение, динамическое программирование, жадный алгоритм и т.д. Выбор правильного подхода существенно влияет на эффективность алгоритма.
Анализ сложности
Перед реализацией алгоритма оцените его временную и пространственную сложность. Это поможет предвидеть эффективность алгоритма ещё до его написания. Временная сложность относится к количеству времени, которое алгоритму нужно для выполнения, в зависимости от размера входных данных, а пространственная сложность — к объёму памяти, который требуется для его работы.
Примеры решения задачи
Рассмотрим задачу нахождения двух чисел в массиве, которые в сумме дают заданное число. Это классическая задача, которая может быть решена несколькими способами с разной степенью эффективности.
1. Неоптимизированный подход
Наиболее прямой, но наименее эффективный способ — использовать двойной цикл для перебора каждой пары чисел и проверки их суммы.

Этот метод имеет временную сложность O(n^2), где n — размер массива, и пространственную сложность O(1).
2. Подход с использованием хэш-таблицы
Этот метод значительно ускоряет поиск, используя хэш-таблицу (в Python это словарь) для запоминания пройденных чисел и их индексов.
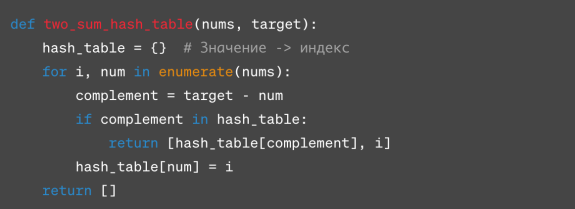
Этот алгоритм имеет временную сложность O(n), так как каждый элемент массива посещается не более одного раза. Пространственная сложность также O(n) из-за использования дополнительной памяти для хранения хэш-таблицы.
3. Оптимизированный подход с сортировкой
Ещё один способ решения — сначала отсортировать массив, а затем использовать два указателя для нахождения нужных чисел.

Этот метод требует времени O(n log n) из-за сортировки и O(n) дополнительной памяти для хранения индексов и значений. Он эффективнее первого метода, но может быть менее эффективным по сравнению со вторым в зависимости от размера входных данных и особенностей реализации сортировки.
алгоритмы
программирование
python