Математика в 3Д ► 05. Практика

Сегодня - практика, чтобы закрепить материал предыдущих уроков - урок 1, урок 2, урок 3, урок 4.

Буду очень благодарен всем, кто решит стать платными подписчиками или разово задонатить на означенные цели. Это сильно мотивирует на продолжение.

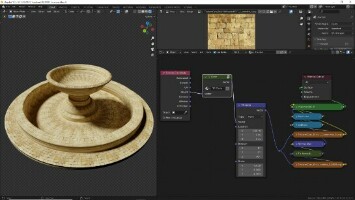
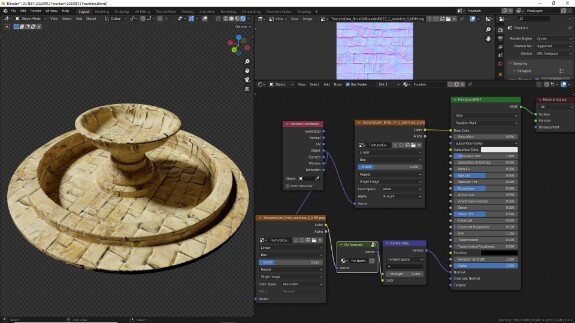
Для примера возьмём простую модель фонтана:

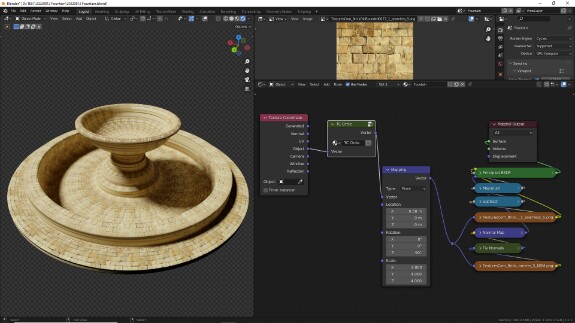
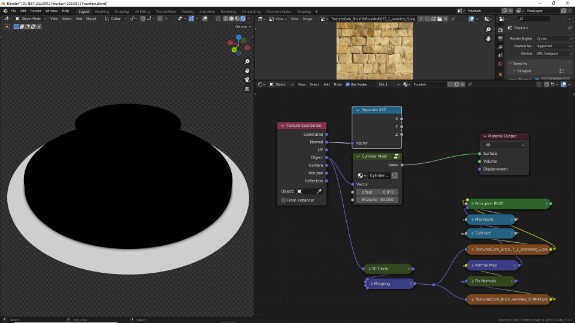
↑ В Shader Editor добавим материал.

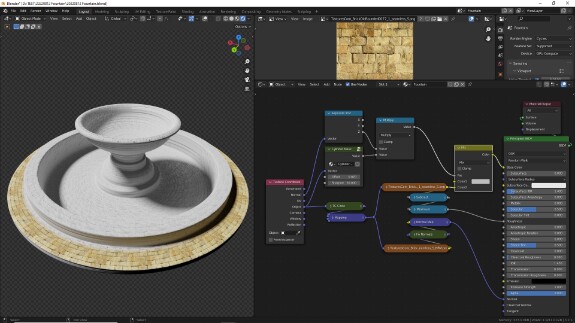
↑  Для начала настроим шейдер. Подключим Image Texture в качестве Base Color к Princinpled BSDF и откроем в нём файл, скачанный отсюда. 

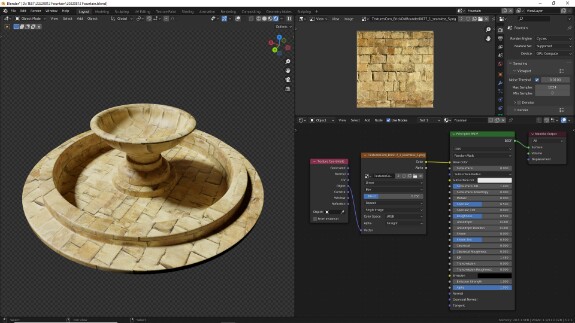
↑ Поскольку UV-развёртка модели сделана весьма топорно, чтобы от неё не зависеть, мы будем использовать более универсальную систему координат - Object. В отличие от системы координат UV, Object - трёхмерная система координат. Это значит, что UV определяет значения только по осям X и Y, а Object - ещё и по Z. Для того, чтобы использовать двухмерную текстуру в трёхмерной системе координат, её надо спроецировать на каждую пару осей. Звучит сложно, но делается в один клик: просто меняем в настройках Image Texture Flat на Box. Так текстура будет проецироваться на поверхность объекта с шести сторон (слева, справа, сзади, спереди, сверху, снизу) - в зависимости от направлений нормалей объекта. Добавляем параметр Blend, чтобы немного смазать границы на стыках этих сторон.

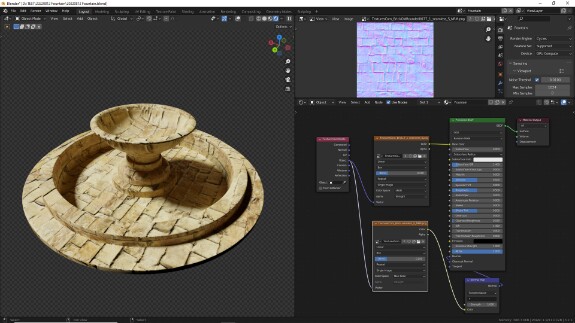
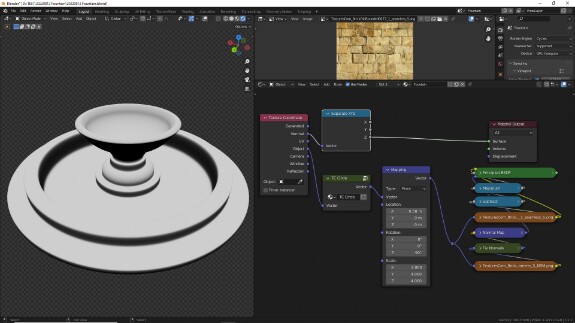
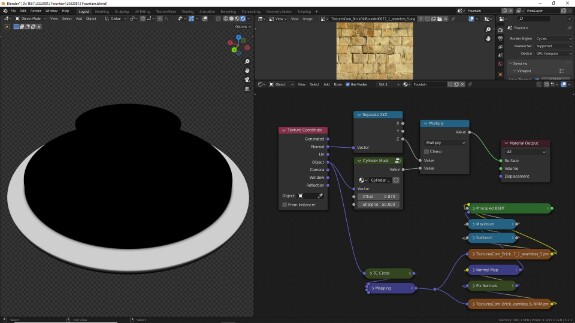
↑ Опционально с помощью Image Texture в слот Normal Principled BSDF через Normal Map можно подключить карту нормалей.

Файла с картой нормалей на сайте нет, приложить её не могу из-за лицензии и авторских прав, но её можно очень легко сгенерировать из первой текстуры, например, в Materialize для Windows, в Gimp - как показано здесь или в каком-нибудь онлайн-конверторе. Image Texture с картой нормалей будет использовать ту же систему координат и те же настройки, что и первая текстура, за исключением того, что её Color Space нужно переключить на Non-Color.

🛈 Техническое объяснение, зачем это делать, для любителей технических объяснений. В Normal Map цветовая информация, а точнее, числовые значения, определяющие яркость Красного, Зелёного и Синего каналов, используется не как цвет, а непосредственно как числовые значения, а именно, как векторы, переопределяющие направление и длину исходных векторов нормалей поверхности объекта. Поэтому для правильного отображения нужно использовать их реальные величины. А цветовое пространство sRGB, повсеместно использующееся для отображения цветов на мониторах с 1996 года, отображает цветовую информацию не линейно, а с корректирующей матрицей, для удобства визуального восприятия, с учётом физиологических особенностей человеческого зрения. С очень существенно корректирующей матрицей. То есть Image Texture, когда Color Space выставлен на sRGB, на выходе выдаёт не исходные, а уже скорректированные значения для красного, зелёного и синего каналов. Кстати, для тех, кто почувствовал, что его всё это время обманывали, подсовывая ненастоящие цвета и мешая стать сверхчеловеком, посмотреть, как цвета выглядят при их линейной репрезентации можно, если перевести Color Space в режим Linear. Такое себе, да.

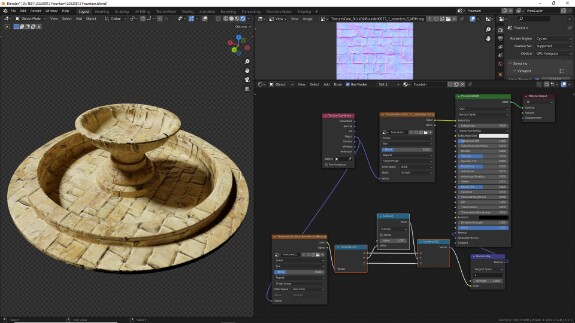
↑ Разные рендер-движки могут по-разному считывать средний канал карт нормалей. В Blender все рендер-движки интерпретируют этот канал как +Y, а, например, Unreal Engine - как -Y. Если вам попалась карта нормалей для игрового движка - вы уже переключили цветовое пространство на Non-Color, подключили её к шейдеру через Normal Map, а поверхность объекта всё равно отображается как-то неправильно, как будто вывернута наизнанку - это решается с помощью инвертирования среднего канала карты. Для этого разделяем каналы с помощью Separate XYZ. Обратите внимание, что поскольку мы работаем с числовыми значениями, а не с цветом, мы используем Separate XYZ, а не Separate RGB. После разделения инвертируем значения среднего канала, вычтя их из единицы с помощью Math в режиме Subtract и снова собираем результат с помощью Combine XYZ.

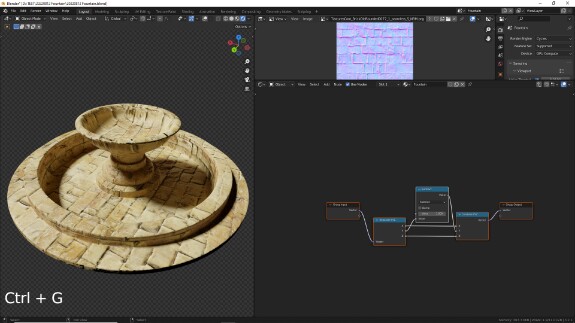
↑ Чтобы эта связка нодов не мешалась, выделяем их и нажимаем Ctrl+G, чтобы создать группу. Заходить и выходить в созданные группы можно с помощью Tab.

↑ Выходим из группы с помощью Tab и переименовываем её во что-то осмысленное и читаемое, например - Fix Normals (исправить нормали)

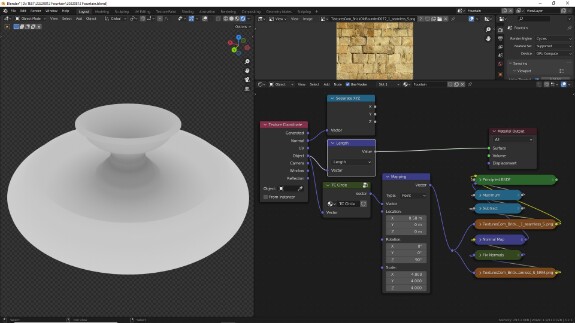
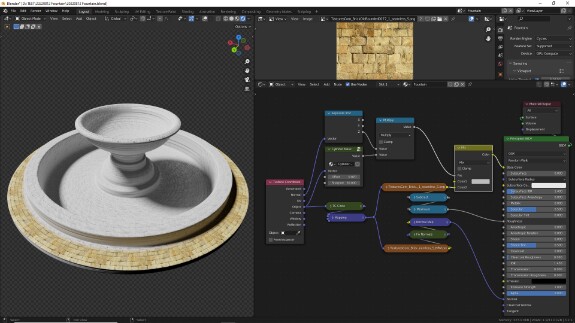
Следующий аспект - параметр Roughness. Идеально гладкие объекты могут существовать только в альтернативных вселенных (осторожно, мат). В реальной жизни всё, что нас окружает, имеет небольшие, микроскопические и не очень, потёртости, шероховатости, загрязнения. В Principled BSDF это реализовано с помощью параметра Roughness. Когда он равен нулю, отражения на поверхности идеальные, без каких-либо искажений, угол падения равен углу отражения, всё чётко. При добавлении Roughness отражения начинают расплываться, как когда в ванной комнате зеркало покрывается паром. Следует иметь в виду, что отражают в той или иной мере любые поверхности, не только зеркала и стёкла, а вообще любые - камни, ткани, немытая полгода машина. Но соотношение отражаемого и поглощаемого света и уровень Roughness у материалов разные. Мало того, уровень мутности/шероховатости на любой поверхности редко бывает однородным. Поэтому для создания реалистичных материалов параметр Roughness чаще всего регулируется не числовым значением, а текстурами, которые для каждой точки поверхности задают её собственное числовое значение. Чёрный - это 0 (полностью гладкий), белый - это 1 (полностью размытые отражения), оттенки серого - значения Roughness от 0 до 1.

↑ В этом примере мы будем использовать для Roughness ту же текстуру, что и для цвета. Но в исходном виде её самый тёмные участки - то есть наиболее близкие к нулю, то есть, получается, потенциально наименее шероховатые (наиболее гладкие) - приходятся на трещины, а логичнее было бы всё же сделать наоборот. Поэтому предварительно мы инвертируем эти значения, вычтя их из 1 с помощью Math в режиме Subtract. И поскольку камни шероховатые и уровень Roughness у них в любом случае высокий, дополнительно ограничиваем минимальные значения с помощью Math в режиме Maximum. Таким образом, если значения текстуры окажутся ниже порога, который мы укажем, то будет использовано максимальное из двух чисел, а именно - сам порог.

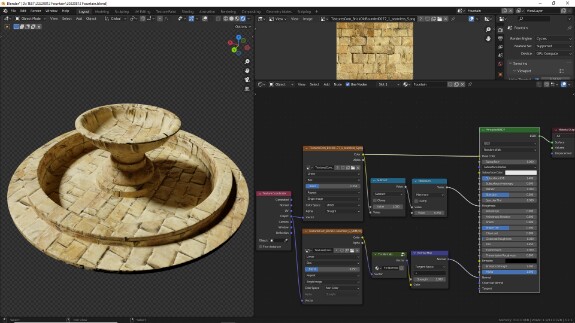
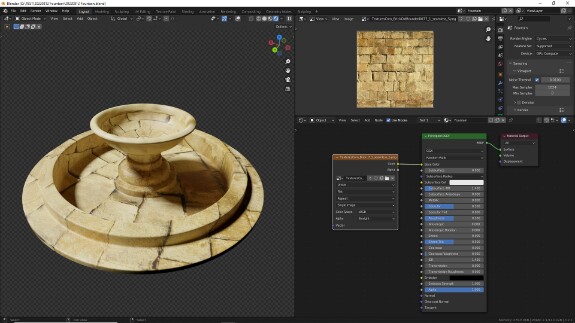
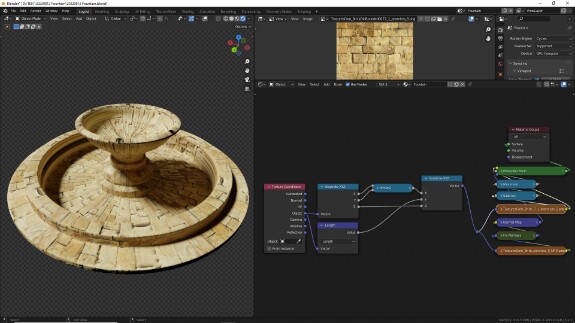
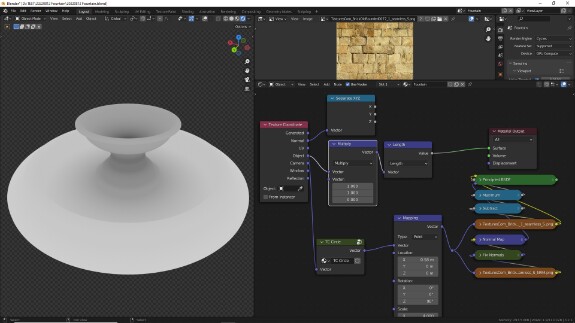
↑ В результате настроенный шейдер выглядит так.

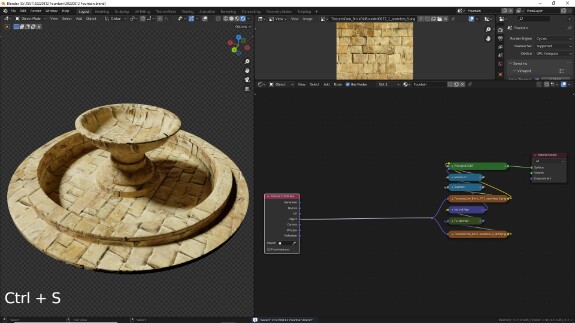
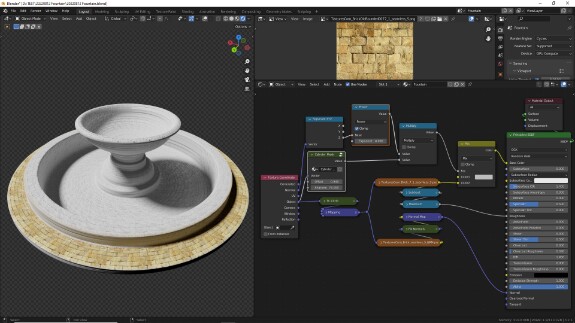
↑ Поскольку мы пока больше не будем трогать эти настройки, отключаем у них неиспользуемые входы и выходы, выделив их и нажав Ctrl+H (вернуть их, если что, можно, нажав то же самое повторно). Сворачиваем их с помощью H (развернуть - тоже H) и переаранжируем их так, чтобы они не занимали много места.

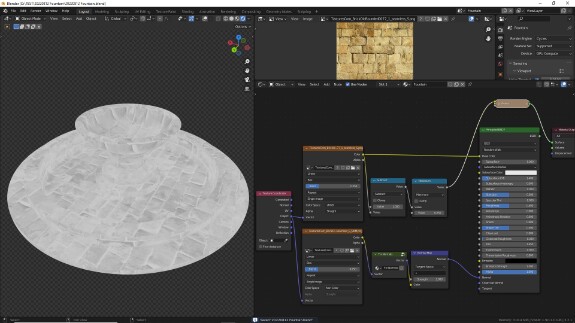
Сейчас текстура располагается так, как и была спроецирована изначально, наша задача - на отдельных участках объекта, где это выглядит логичным, расположить её по кругу. Для этого нам нужно изменить с помощью векторной математики систему координат. Давайте для начала посмотрим, как распределяются значения её осей координат и соотнесём с тем, как отображается текстура на скриншотах выше:

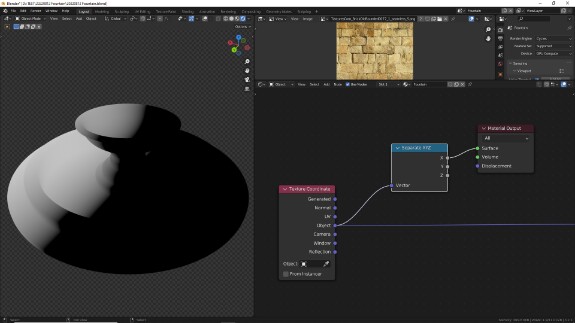
↑ Ось X. Во вьюпорте мы смотрим на объект сзади, поэтому ось X идёт справа налево, от минусовых значений (где всё чёрное), через ноль (в центре объекта, рядом с линией, на которой градиент только-только начинает светлеть) к положительным значениям (где градиент приближается к белому цвету)

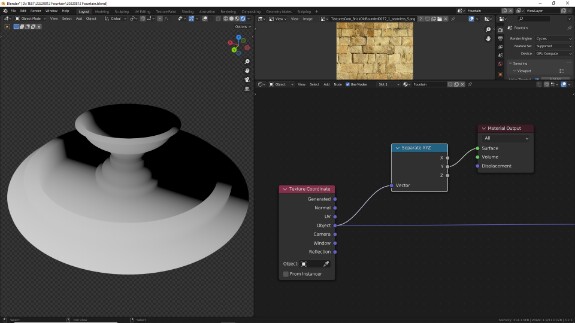
↑ Ось Y. Опять же, поскольку мы смотрим на объект сзади, ось Y идёт по направлению от заднего края к переднему. Чёрное - минусовые значения и ноль, серый градиент - постепенно увеличивающиеся значения

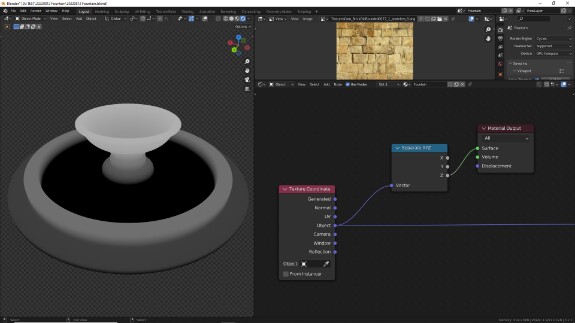
↑ Ось Z. Располагается снизу вверх

При таком распределении значений текстура проецируется на объект, как мы видели тремя скриншотами выше. Направление полосок кирпичей совпадает с осью Y и перпендикулярно оси X. 

Но оси координат совершенно не обязаны выстраиваться в одну линию, они могут представлять из себя совершенно разные кривые, формы и фигуры. Как бы они ни искривлялись, текстура будет растянута по ним, в соответствии с их числовыми значениями, где бы те ни находились. То есть если мы, например, хотим расположить текстуру по кругу, мы можем создать новую систему координат, в которой сама ось X будет расположена по кругу. Иными словами, нам нужно, чтобы градиент от черного к белому располагался по кругу... И мы как раз уже такое проделывали в самом первом уроке (как удачно!)

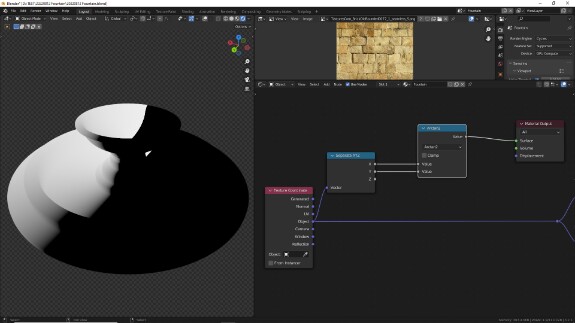
↑ Для этого нам нужно взять две перпендикулярные оси - в данном случае X и Y - и подключить их к ноду Math в режиме Arctan2

↑ 🛈 Если бы нам вдруг понадобилось привести значения градиента к диапазону от 0 до 1 (нам это не понадобится, мы так не будем делать, но если бы делали) - нам нужно было бы сначала прибавить к исходным значениям с помощью Math в режиме Add число Пи (его необязательно помнить наизусть или гуглить, достаточно просто вбить слово pi - и Блендер подставит число автоматически). Таким образом мы бы вывели все значения в положительный диапазон. И так как исходные значения, получается, были в диапазоне от -Пи до Пи, для нормализации диапазона, нам нужно было бы разделить результат на 2Пи с помощью Math в режиме Divide. Это значение можно вбить как pi*2.

Приводить систему координат к диапазону от 0 до 1 мы не будем, поскольку как систему координат её от этого только растянет, но суть не поменяется. Оставим её пока в том виде, в котором она выходит из Arctan2. Но это у нас, напомню, только ось X, а нам для проекции нашей двухмерной текстуры нужна ещё ось Y. И если ось X опоясывает объект по кругу, то ось Y, чтобы быть перпендикулярной оси X, логично, должна идти из центра круга наружу. Иными словами, для оси Y нам нужен градиент, который в центре объекта был бы тёмный, а к краям светлел. Ничего не напоминает?

↑ Именно! Радиальный градиент - это Vector Math в режиме Length - измерение длины вектора, которая в центре системы координат равна нулю (или чёрному цвету), а чем дальше от центра, тем становится больше (белее).

↑ Нам остаётся сформировать из получившихся осей новую систему координат, используя нод Combine XYZ. В качестве оси Z мы будем использовать оригинальную необработанную ось Z.

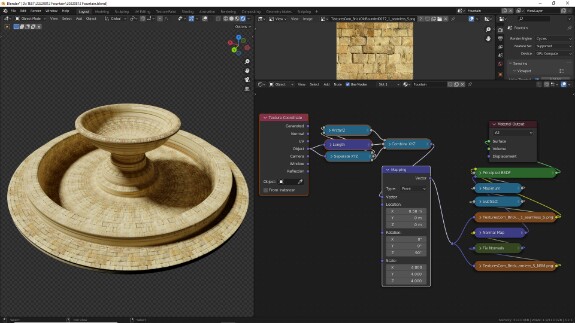
↑ Смещением, размером и вращением получившейся системы координат мы можем управлять с помощью нода Mapping. Обратите внимание, что изменения оси X будут изменять текстуру по кругу, а по оси Y - от центра круга к краям.

↑ Для компактности уберём получившийся конвертор текстурных координат внутрь отдельной группы, выделив все нужные ноды и нажав Ctrl+G. Напомню, что выйти и зайти в группу можно с помощью Tab.

Теперь, просто для примера, посмотрим, как работать с масками. Мне нравится, как с такими настройками текстура выглядит на внешней дорожке вокруг фонтана, и я бы хотел её такой здесь и оставить. Остальные части мне нравятся меньше: ближе к центру текстура становится слишком мелкой, а если внимательно присмотреться к тем фрагментам объекта, которые направлены в стороны, а не вверх, то можно заметить сильные искажения, появившиеся из-за того, как мы стали проецировать текстуру.

Я не буду в этом уроке обрабатывать весь фонтан. Была такая попытка, но после 50 скриншотов, разросшегося во весь экран нодового дерева и примерно четверти от всей работы стало понятно, что для урока это перебор. Поэтому я просто продемонстрирую на практике основные принципы и логику. Если будет желание - можете потом продолжить и доделать всё полностью уже самостоятельно - как сочтёте нужным.

Итак, задача - оставить дорожку вокруг фонтана, точнее ту её часть, которая смотрит вверх, и сделать так, чтобы всё остальное можно было регулировать отдельно, независимо от неё.

Мы сможем использовать нод MixRGB, чтобы смешивать текстуры с разными настройками. Когда его вход Fac (Factor) равен 0, он возвращает только текстуру или цвет или числовые значения (что суть одно и то же), подключенные в верхний слот. Когда его вход Fac (Factor) равен 1, он возвращает только то, что подключено в нижний слот.

Если мы подключаем к Fac черно-белый градиент, то в тех местах поверхности объекта, где этот градиент черный (то есть равный 0), будет отображаться то, что подключено в верхний слот, а в тех местах, где градиент белый (то есть равный 1), будет отображаться то, что подключено в нижний слот.

То есть, чтобы оставить нетронутой дорожку, нам нужно сделать такой градиент, чтобы белой осталась только дорожка, а всё остальное было чёрным. Тогда мы сможем подключить в нижний слот то, что уже успели сейчас сделать, а в верхний - то, что будем настраивать по-другому. 

Поехали!

Для начала отделим все части, которые смотря вверх. Из урока про текстурные координаты мы можем знать, что текстурные координаты Normal, если их разделить на отдельные оси, окрашивают в белый цвет те части поверхности объекта, направление нормалей которых совпадает с направлением соответствующих осей:

↑ Используем выход Normal из нода Texture Coordinates и выход Z из нодa Separate XYZ, чтобы белыми стали все поверхности, нормали которых совпадают с направлением оси Z, то есть смотрят вверх.

Теперь нам надо убрать лишнее, то есть в получившемся градиенте всё, что ближе к центру, чем дорожка, окрасить в чёрный. Чёрный, напомню, это 0, а белый - 1. Вспоминаем урок 4 - чтобы сделать белый цвет чёрным, можно либо вычесть из него 1 (то есть сделать центр белым, а края чёрными и вычесть это из нашего градиента с помощью Math в режиме Subtract), либо умножить на 0 (то есть сделать центр чёрным, а края белыми и умножить на это наш градиент с помощью Math в режиме Multiply).

Умножение на 0 в общем случае использовать надёжнее. Потому что вычитая что-то из чего-то, мы рискуем уйти в область минусовых значений, и это может в какие-томоменты выйти боком. А умножение на 0 всегда даёт 0, что с ним ни делай. Поэтому будем использовать умножение, а значит, нам нужно закрасить центр чёрным, а края оставить белыми.

↑ Мы уже делали в этом уроке чёрно-белый градиент от центра к краям - это делается с помощью Vector Math в режиме Length, это один из наиболее часто используемых нодов для круглых, цилиндрических и сферических масок.

↑ Поскольку длина вектора высчитывается по всем трём осям, Length из текстурных координат Object рисует не круг, а сферу вокруг центра объекта. То есть если продлить геометрию из середины объекта выше (или ниже), то с удалением от центра она также постепенно начнёт белеть. Чтобы этого избежать, перед Length мы поставим нод Vector Math в режиме Multiply, и с его помощью умножим текстурные координаты по осям X и Y на 1, а по Z - на 0. При умножении на 1 значения, как мы знаем, не меняются, а при умножении на 0 они становятся равными 0, таким образом ось Z бесконечно растягивается в пространстве одно и то же значение, которое находилось в центре системы координат - а именно, 0 -  и получается, что градиент у нас уже не сфера, а бесконечный цилиндр, растянувшийся вдоль оси Z.

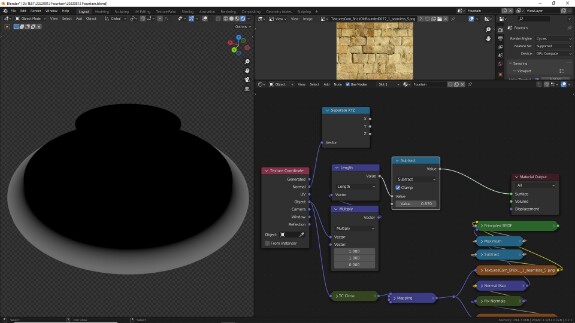
↑ Вспоминаем, что это не просто градиент, а числовые значения, и нам надо, чтобы значения, равные 0, начали распространяться дальше от центра. То есть нам надо придумать, как последовательно воздействовать на положительные значения, чтобы постепенно приводить всё больше их к нулю. Это можно сделать с помощью нескольких математических операций, но в данном случае проще всего банально производить вычитание с помощью Math в режиме Subtract с галочкой Clamp. Таким образом всё больше и больше значений начнет проваливаться в минус, а с помощью Clamp мы ограничим выходной диапазон нулём и единицей, и всё, что ниже нуля будет становиться нулём. А 0 это чёрный, а чёрный в центре - это то, что нам нужно. Бинго!

Граница, однако получается слишком размытая, чтобы дорожка осталась чёткой, нам нужно свести переход от чёрного к белому к минимуму. Мы вообще могли бы использовать, например, Math в режиме Greater Than, и граница у нас была бы абсолютно чёткой. Но мне бы хотелось всё же, чтобы был некий запас размытости этой маски, чтобы была узенькая полоска перехода от чёрного к белому - это позволит лучше смиксовать материалы на границе маски.

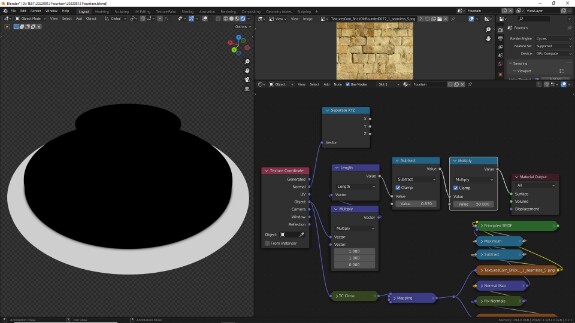
↑ Для этого, настроив предварительно вычитание таким образом, чтобы вся область, которая должна быть нулём, стала им, чтобы нам постепенно начать увеличивать оставшиеся значения, постепенно приводя их ближе к единице, мы можем выполнить... какое математическое действие? Вычитание уже было, деление будет их уменьшать, сложение добавит к нулю значения и он перестанет быть нулём. Остаётся умножение. Умножая любое число на 0, мы получаем 0, поэтому 0 в центре так им и останется, а все значения выше 0 постепенно начнут увеличиваться. Конечно, они начнут увеличиваться и выше 1, но для этого мы опять же можем использовать галочку Clamp. Умножение, напомню, это Math в режиме Multiply

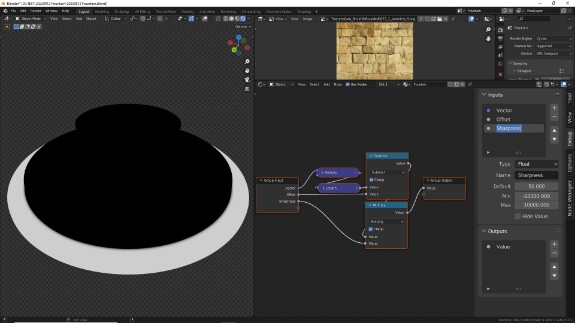
↑ Поскольку получившуюся цилиндрическую маску мы можем с незначительными изменениями потом использовать в этом объекте и для определения других областей, целесообразно собрать её в группу (Ctrl+G) и вывести в качестве наружных параметров управления смещение маски от центра - то, что делает Subtract, - и чёткости границы - то, что делает Multiply. Чтобы добавить новый наружный параметр управления, надо внутри группы подключить свободный нижний слот в Group Input к нужному параметру нужного нода. Так у группы снаружи появится дополнительный ползунок с соответствующим типом значения. Внутри группы в N-панели (вызывается по нажатию клавиши N) во вкладке Group можно переназывать входы, менять их местами, задавать минимальные и максимальные значения.

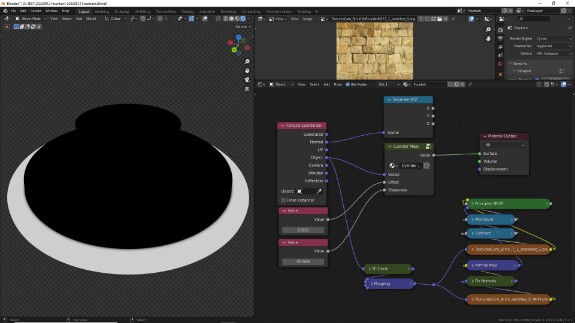
↑🛈 Чтобы группа автоматически создалась со всеми нужными входами, можно перед её созданием предварительно подключить к нужным параметрам объединяемых у группу нодов ноды Value с нужными значениями. При создании группы ноды Value должны остаться вне группы, тогда линки от них образуют новые входы. Если несколько параметров нодов управляется одним значением, то чтобы не создалось лишних входов, перед упаковкой в группу можно объединить линки таких нодов с помощью Reroute - точек перенаправления линков. Это можно сделать, если удерживая Shift и зажатую правую клавишу мыши провести мышью по нужным линкам. Для этого в Edit > Preferences > Add-ons должен быть включён аддон Node Wrangler (включён в Блендер, находится через поиск в меню аддонов, активируется галочкой). После создания группы ноды Value можно удалить, и управлять параметрами группы уже в самой группе ↓

Так... Что мы делаем? Ах да! Мы создавали две разные маски. Одну - заливающую белым все поверхности, направленные вверх. Вторую - бесконечным цилиндром заливающую чёрным центр. Теперь нам надо их перемножить

↑ Перемножаем две маски с помощью Math в режиме Multiply. Может быть не очень заметно, но таким образом мы оставили мягкие края при переходе на вертикальные поверхности, а сами вертикальные поверхности остались чёрными.

↑ Используем результат в качестве фактора смешивания в ноде MixRGB. Похоже, успех: всё работает. Дорожка остаётся дорожкой, а верхний цвет в MixRGB мы контролируем отдельно.

↑ Пока не пошли дальше, корректируем маску по нормалям, добавляем ей жёсткости, возводя все её значения в степень 4 с помощью Math в режиме Power

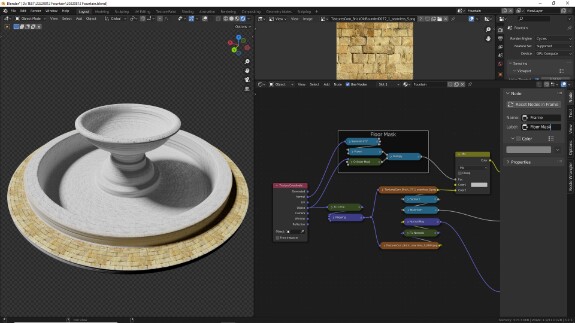
↑ Реорганизуем и группируем ноды, чтобы поддерживать порядок в проекте. Компактизируем, Ctrl+H, H, добавляем им рамочку с помощью Ctrl+J и в N-панели во вкладке Node в графе Label задаём рамочке название

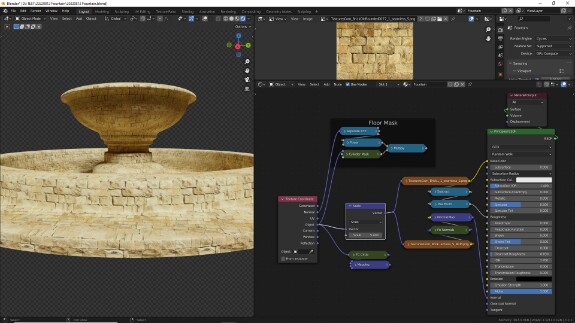
↑ Временно отключим от векторных входов в текстуры нашу кастомную систему координат и настроим другую. Возьмём исходную систему координат Object и с помощью Vector Math в режиме Scale увеличим систему координат, визуально уменьшая текстуру. Чтобы понять, почему так происходит, подумайте, как при увеличении значений системы координат меняется их местоположение.

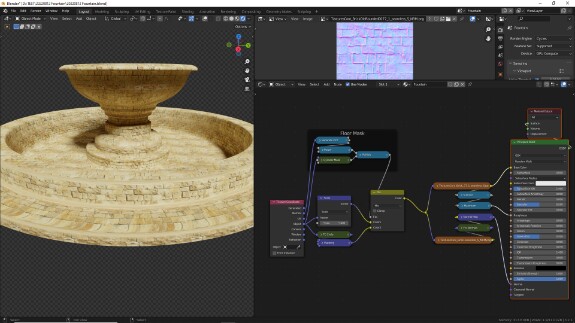
↑🛈 В отдельных случаях, чтобы не использовать повторно множество одних и тех же текстур, загружая ресурсы компьютера, бывает уместно смешать не сами текстуры, а системы координат. Но в данном случае, поскольку мы использовали маску с мягкими краями, то как раз на этих местах перехода получаются некрасивые искажения. Это происходит потому, что одна система координат плавно перетекает в другую, в местах перехода создавая множество промежуточных систем координат - или, если рассматривать с другой точки зрения, одну большую вывернутую и искаженную третью систему. Поэтому в данном случае, чтобы получить ровные переходы, нам придётся полностью продублировать все текстуры и смешивать уже готовые цветовые результаты ↓

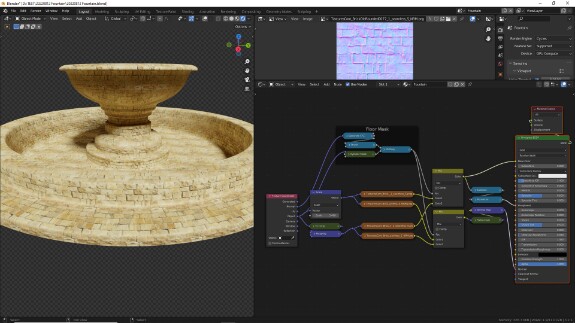
Для пущего эффекта можно с помощью простой векторной математики подогнать первую систему координат под вторую - здесь речь о стыках дорожки с сопряжёнными вертикальными откосами ↓

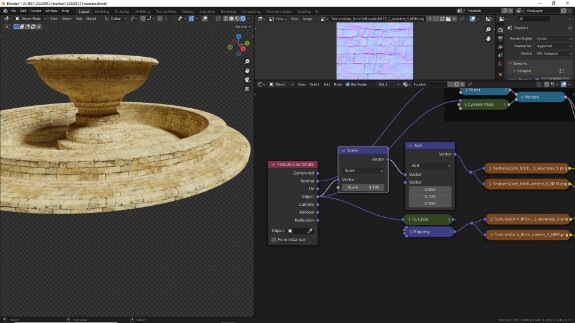
А дальше остаётся только продолжать в том же духе - делать маски, добавлять и подмешивать новые наборы текстур (для каких-то частей, возможно, вообще других), подгонять их друг под друга - и так пока вы не сочтёте результат приемлемым, а материал объекта идеальным.

А если вы прошли этот урок и ничего про него нигде не написали, и ни с кем не поделились и не лайкнули даже, то фу-фу-фу на вас. Ну вот как так можно?..

← ПРЕДЫДУЩИЙ УРОК    СЛЕДУЮЩИЙ УРОК →