Математика в 3Д ► 09. Voronoi Texture
Voronoi Texture использует в основе своего паттерна диаграмму Вороного, а именно, Георгия Феодосьевича Вороного (1868-1908), одного из создателей новой области математики - геометрии чисел. Главным её создателем, к слову, был Герман Минковский (1864-1909), имя которого также присутствует в Voronoi Texture в названии одного из видов метрики. Мало того, как мы убедимся, все остальные виды - это только частные случаи метрики Минковского, но об этом позже.
Как генерируется диаграмма Вороного.
Я вкратце опишу алгоритм построения. Для практической художественной работы с Voronoi Texture это знать не то чтобы сильно обязательно, но это однозначно поможет пониманию, что делает каждый из используемых в ней режимов и алгоритмов.
• Сначала в N-мерном пространстве (2D, 3D, 4D и т.д.) псевдослучайным образом задаётся множество точек. Простыми словами - в пространстве генерируются рандомные точки. Это будут центры ячеек.
• Затем между каждой парой точек вычисляется, в зависимости от количества измерений, другое N-минус-один-мерное пространство (линия для 2Д, плоскость для 3Д и т.д.), равноудалённое от обеих точек и перпендикулярное линии между ними. Простыми словами - между точками на равном расстоянии от каждой из пар выстраиваются стенки. Это будут стены ячеек.
• Сами ячейки, если говорить о базовом случае - это визуальная репрезентация расстояния в пространстве до ближайшей точки, где 0 - это чёрный цвет, а 1- белый. Простыми словами - расстояние до ближайшей точки отображается в Voronoi Texture в виде чёрно-белого градиента: ближе к центру расстояние до точки равно 0, поэтому там они чёрные, а ближе к краям стремится к 1, поэтому там они светлеют.
Желающим подробнее углубиться в математику принципов построения диаграммы Вороного можно начать отсюда.
Особенности применения диаграммы Вороного в Voronoi Texture.
Стоит иметь в виду, что центры ячеек и их стенки для всех алгоритмов остаются неизменными. Однако, помимо базового случая, существует как несколько вариантов того, какое именно расстояние вычисляется и отображается (первый сверху параметр, по умолчанию F1), так и того, в какой метрике происходит вычисление (второй сверху параметр, по умолчанию Euclidian). Все возможные комбинации, которые предоставляет Voronoi Texture мы рассмотрим ниже.
Диапазон значений.
Поскольку во всех алгоритмах Voronoi Texture измеряется расстояние от чего-то до чего-то, нижняя граница диапазона значений равна 0 (расстояние не может быть отрицательным). Верхняя может существенно меняться, в том числе выходя далеко за пределы 1, в зависимости от того, что именно измеряется и каким методом.
Практическое применение Voronoi Texture в компьютерной графике.
В художественном плане для нас важно, что Voronoi Texture представляет из себя ячейки. Все паттерны, структура которых может быть интерпретирована, как ячейки - любые пористые структуры, пузырьки в жидкостях, растрескавшаяся земля в пустыне, окрас шерсти жирафа или леопарда, звёзды на небе - генерируются с помощью Voronoi Texture. Разглядели в стоящей перед вами задаче нечто, хотя бы отдалённо напоминающее ячейки - вспомнили о Voronoi Texture.
🛈 Также с помощью ячеек Voronoi работают практически все симуляции, связанные с "раскалыванием" объектов на обломки, они могут использоваться, как основа для симуляций дымов, часто используются при распознавании объектов в 3D-сканировании. Использование диаграммы Вороного выходит далеко за пределы компьютерной графики и имеет широкое применение в метеорологии, гидрологии и многих других, возможно, неожиданных на первый взгляд областях.
Структура проекта.
Как и в предыдущих уроках, используются текстурные координаты типа Object (в Geometry Nodes - Position). Слева направо показаны:
• Сдвиг вертексов относительно нормалей с помощью геометрических нодов
• Срез на плоскости
• 5 срезов, на небольшом расстоянии, наложенных друг на друга
• трёхмерный волюметрик материал
Подробнее про то, как настроен проект, здесь.
Буду очень благодарен всем, кто решит стать платными подписчиками или разово задонатить на означенные цели. Это сильно мотивирует на продолжение.
Поехали!
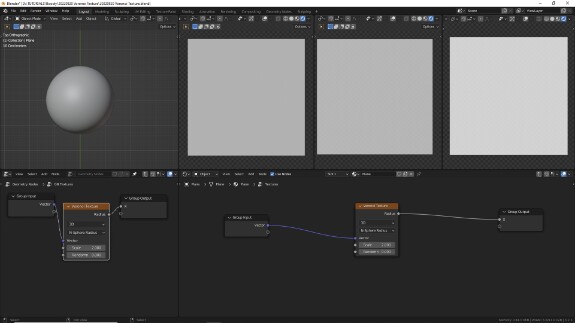
Верхний параметр (по умолчанию - 3D), отвечающий за количество измерений текстуры, работает точно так же, как и в Noise Texture, и в Musgrave Texture, поэтому на нём я останавливаться не буду.
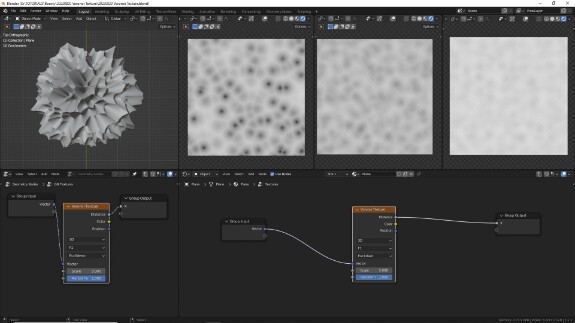
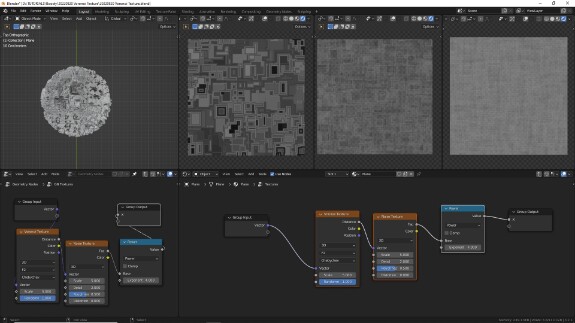
↑ Voronoi Texture с дефолтными настройками:
• 3D - паттерн генерируется в 3-х измерениях
• F1 - отображается расстояние до ближайшей точки
• Euclidian - используется евклидово пространство или линейное измерение расстояния до ближайшей точки
• Scale = 5 - исходный паттерн уменьшен в 5 раз
• Randomness =1 - рандомизация расположения точек в пространстве максимальная.
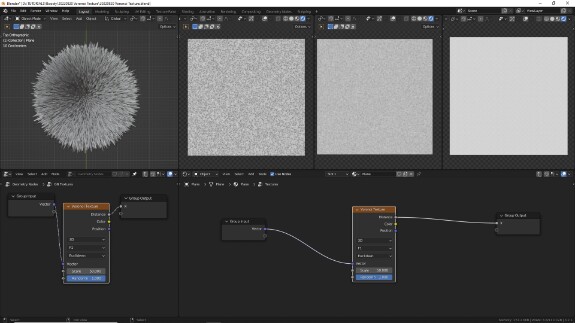
↑ Как и в других процедурных текстурах, параметр Scale меняет размер паттерна, позволяя создавать как очень маленькие ячейки, размером с песчинку...
🛈 Информация к размышлению. Никогда не задумывались, что несколько полупрозрачных плэйнов с единственной Voronoi Texture могут при должной изобретательности заменить или дополнить симуляции с сотнями тысяч частиц - песок, снег, дождь, пузырьки? Обратите внимание на песок и облака в начальной заставке с логотипом Блендер в этом видео, дальше можно не смотреть, там реклама. Так вот, там нет ни одной симуляции физики, это всё анимированные процедурные шумы:
...
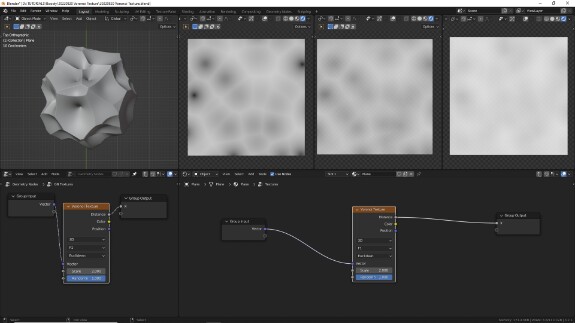
↑ ...так и достаточно крупные, чтобы в сочетании с другими текстурами принимать участие в формировании ландшафта.
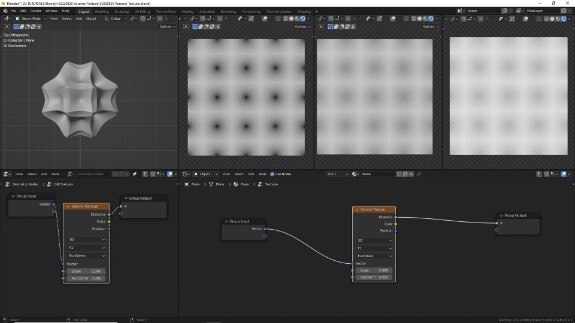
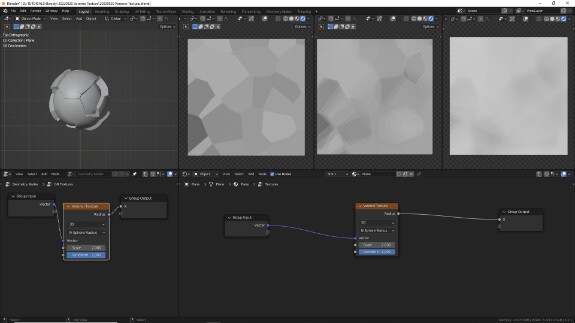
↑ Параметр Randomness определяет уровень рандомизации положения точек. При нулевом уровне Randomness точки, определяющие центры ячеек, выстроены по ровной сетке.
Предлагаю в таком виде, чтобы не отвлекаться на лишние изгибы, которые даёт рандомность, рассмотреть, как одни и те же ячейки с одним и тем же видом рассчёта отображаются при разных способах вычисления этого расстояния, иными словами, при использовании разных метрических систем.
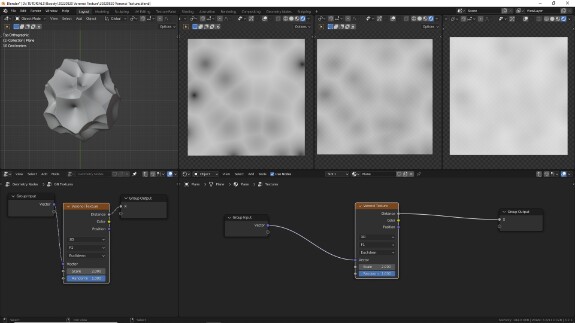
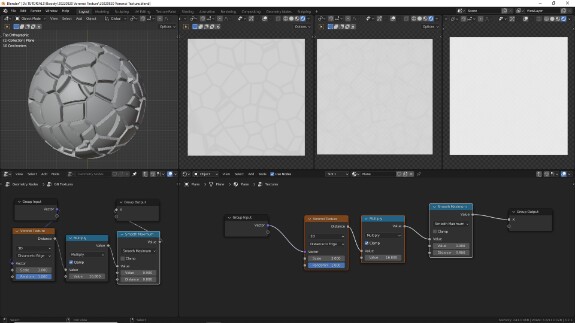
F1
Для начала пройдёмся по типу F1. Он отображает расстояние до ближайшей целевой точки. Помним, что 0 - чёрный, 1 - белый. Поскольку расстояние до точки на месте самой точки равно 0, в центре они чёрные, а поскольку при удалении от точки расстояние увеличивается, к краям они белеют.
На скриншоте выше - отображение расстояния до целевых точек в евклидовой метрике, использующейся по умолчанию. Это линейное измерение расстояния. Примерно то же самое мы делали с текстурными координатами Object с помощью Vector Math в режиме Length.
Рекомендую самостоятельно попробовать использовании на материалах Math в режиме Greater Than, чтобы посмотреть, какой формы будут ячейки в каждом случае. В евклидовой метрике они будут сферами.
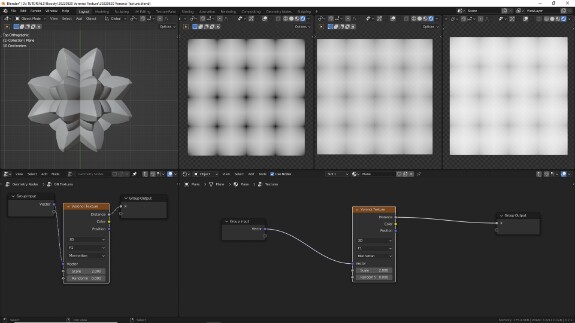
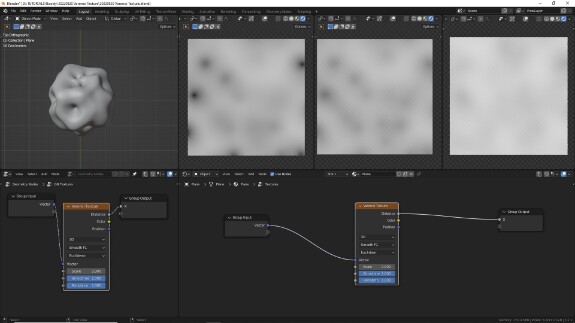
↑ Тот же самый тип F1 (расстояние до ближайшей точки), но уже в манхэттенской метрике. Для тех, кому лень проходить по ссылке и читать статью, сообщаю, что манхэттенская метрика введена в математику Германом Минковским, у которого в Voronoi Texture есть и своя именная метрика, а название "манхэттенская" происходит из-за аналогии с планировкой кварталов на острове Манхэттен.
При манхэттенской метрике, если использовать Math в режиме Greater Than, ячейки будут в форме ромбов.
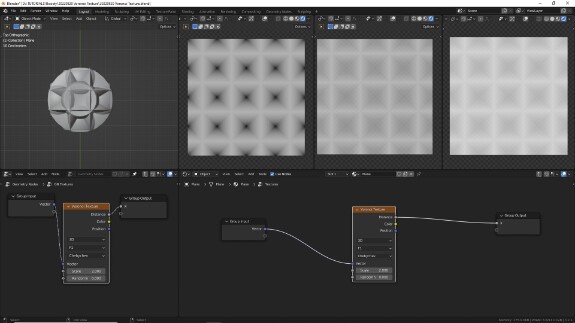
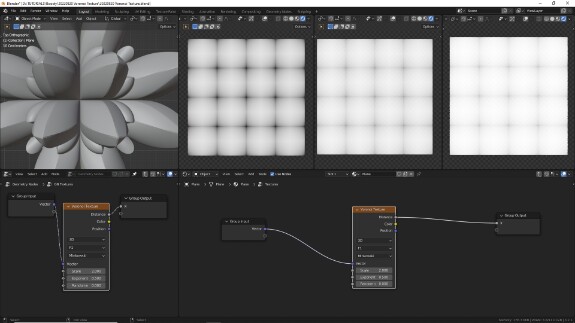
↑ Тот же самый тип F1 (расстояние до ближайшей точки), но уже с использованием расстояния Чебышёва. Просто для справки - шар в этой метрике имеет форму куба, рёбра которого параллельны осям координат, а названа она в честь Пафнутия Львовича Чебышёва (1821-1894), который, как оказалось, Чебышёв, а вовсе не Че́бышев и уж тем более не Че́бычев.
При чебышёвской метрике, если использовать Math в режиме Greater Than, ячейки будут в форме квадратов.
↑ Ну и наконец, F1 (расстояние до ближайшей точки), в метрике Минковского, которая является параметрической и, как можно видеть на графиках в статье, объединяет в себе остальные метрики. У неё есть дополнительный параметр Exponent, по умолчанию равный 0.5 - то есть квадратный корень. Если выставить его на 1 - получится манхэттенская метрика, если на 2 - евклидова метрика, а если примерно на 24 - то очень похожая на чебышёвскую метрика.
Отличия можно увидеть, опять же, с помощью Math в режиме Greater Than. При чебышёвской метрике края у квадратов будут острыми, а при минковской - будут оставаться едва заметно сглаженными.
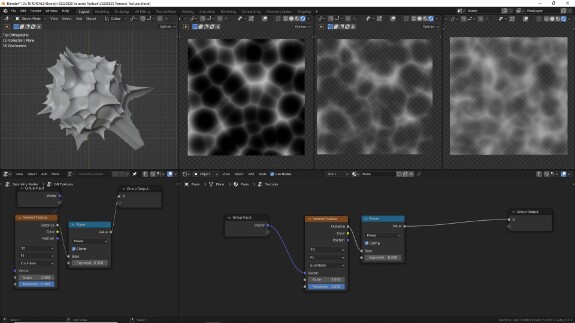
Smooth F1
Следующий по порядку тип измерения - F2, но по логике я бы сначала рассмотрел Smooth F1, потому что это тот же тип F1, но с возможностью сглаживать пиковые значения на месте стенок, делая переходы между ячейками более пологими. Сглаживание осуществляется за счёт параметра Smoothness, который появляется при выборе типа Smooth F1 и представлен в виде фактора, где 0 - сглаживание отсутствует, и результат тот же, что и при использовании F1, а 1 - это полностью сглаженные границы ячеек. Далее - скриншоты типа Smooth F1 в четырёх метриках.
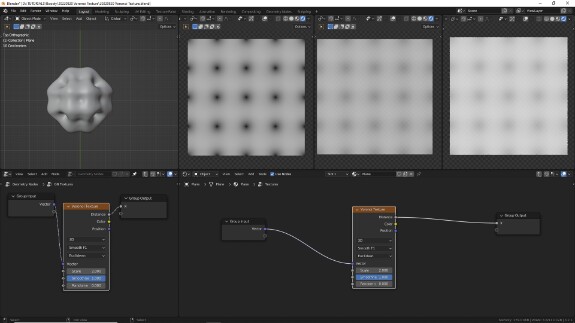
↑ Smooth F1 в евклидовой метрике
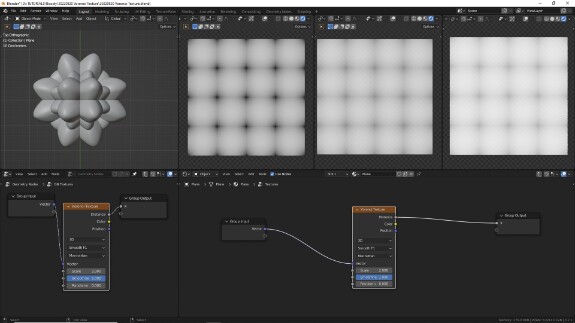
↑ Smooth F1 в манхэттенской метрике
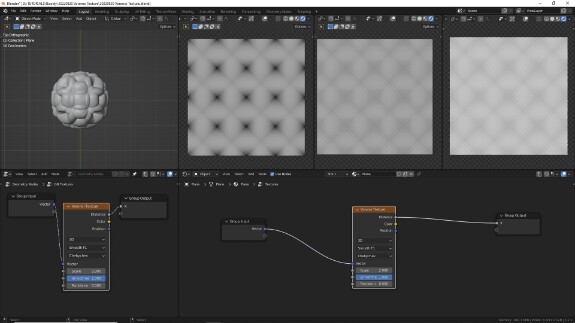
↑ Smooth F1 в метрике Чебышёва
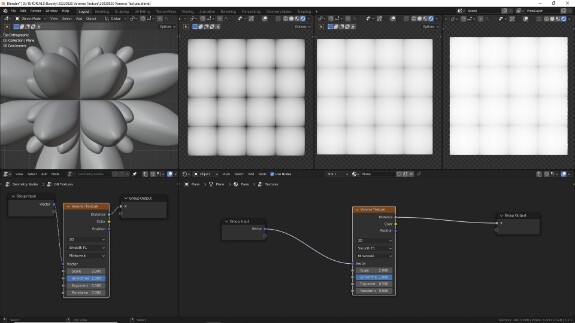
↑ Smooth F1 в метрике Минковского с экспонентой равной 0.5
F2
F2 по смыслу отличается от F1. Если в первом случае измерялось и отображались расстояние до первых ближайших точек, то при F2 отображаются расстояния до вторых ближайших точек. Хорошая зарядка для мозгов - понять, как это происходит.
На практике это делает центр ячейки более светлым - потому что в этом месте расстояние от всех соседних точек максимально, а ближе к стенкам - чуть темнее. При этом, поскольку вторыми ближайшими точками оказываются сразу несколько точек, на стыках лучей, распространяющихся от центров ячеек по направлению к углам, образованным стенками, в градиентах образуются заметные острые грани.
Понять, как это вычисляется, сложнее, чем в случае с F1, и для начала можно просто принять, что с этим алгоритмом получается в 3 раза больше острых граней.
Далее - скриншоты типа F2 в четырёх метриках.
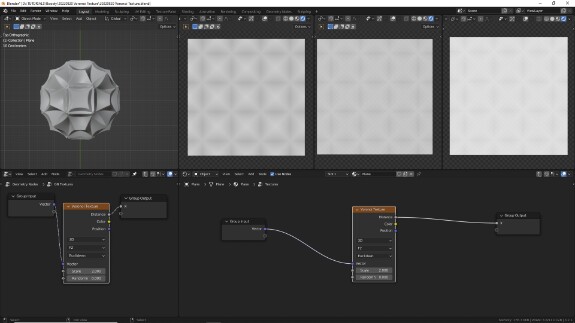
↑ F2 в евклидовой метрике
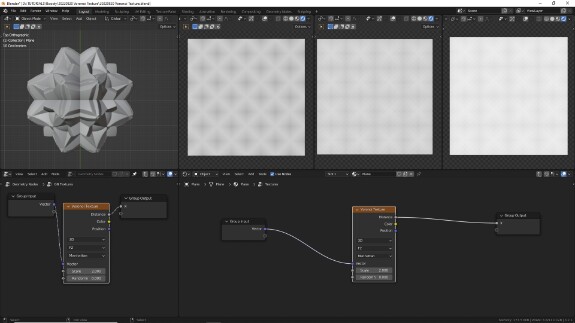
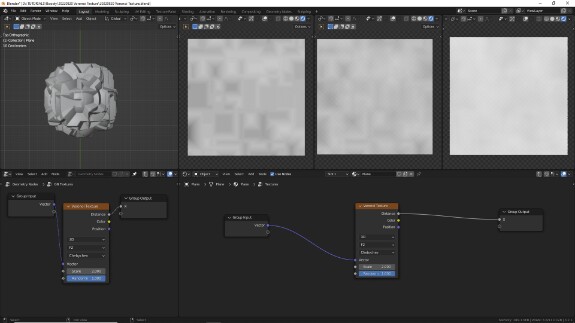
↑ F2 в манхэттенской метрике
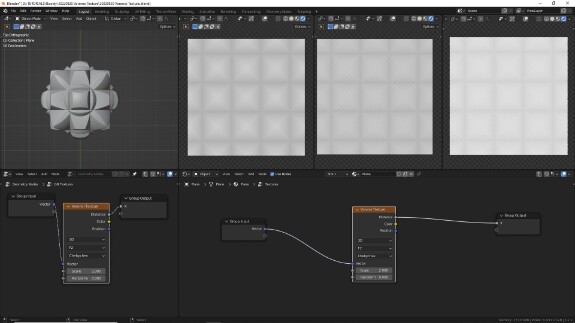
↑ F2 в метрике Чебышёва
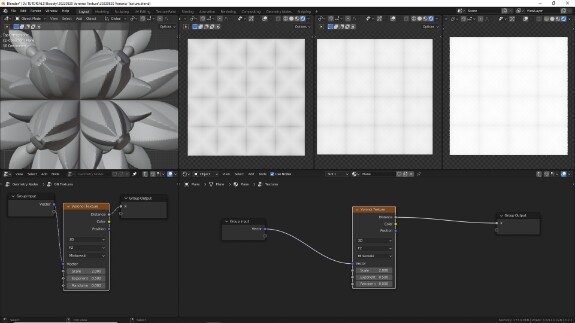
↑ F2 в метрике Минковского
Distance to Edge
В типе измерения Distance to Edge используется только линейная метрика, поскольку измеряется расстояние от краёв ячейки до её целевой точки. В практическом плане с помощью этого типа можно создавать самые тонкие линии из всех процедурных текстур - трещины на земле, молнии и т.п.
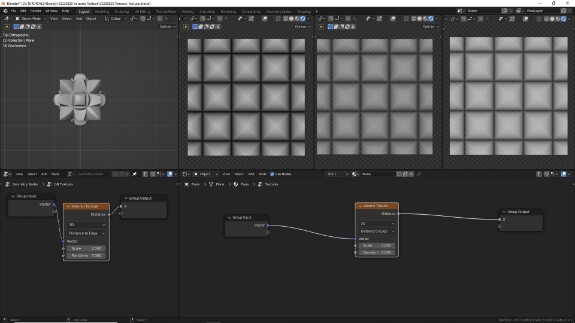
↑ Distance to Edge, как она есть.
N-Sphere to Radius
Согласно документации по Voronoi Texture, это радиус n-сферы, вписанной в ячейки Вороного или половина расстояния между ближайшей целевой точкой и ближайшей к этой точке другой целевой точкой. Переводя на понятный язык этот режим заливает ячейку значением, условно, определяющим её размер. Не могу сказать, что часто этим пользовался. В документации рекомендуют использовать этот режим в паре с Voronoi Texture с теми же настройками Scale и Randomness, но в F1 с евклидовой метрикой, подключенных через Math в режиме Less Than для получения разноразмерных сфер. Вероятно в этом есть смысл, поскольку в чистом виде она может быть применима только в каких-то совсем специфичных случаях.
↑ N-Sphere to Radius при нулевой рандомизации заливает все ячейки одним цветом, поскольку их размер идентичен.
↑ N-Sphere to Radius при максимальной рандомизации заливает каждую ячейку значением, определяющим... давайте я буду называть это "размер ячейки", никто не возражает? Мне кажется, так проще для понимания.
И, раз уж мы заговорили о рандомизации, разумеется, она представляет наверное наибольшую ценность при процедурной генерации материалов с использованием Voronoi Texture (субъективное оценочное мнение). Рассмотрим, как она выглядит в рандомизированном виде чисто внешне, на примере режимов - F1 + Smooth F1 и F2 (расстояние до первой и второй ближайших точки), представленных в 4х разных метриках - Euclidean, Manhattan, Chebychev, Mikowski - и режим Distance to Edges (расстояние от границ ячейки до точки). Со временем вы запомните, какие сочетания дают какие результаты, а пока постарайтесь уловить общие принципы.
↑ F1 + Smooth F1, Euclidean. Внешний вид - ячейки с тёмной серединой и светлыми стенками. Форма - круги (в 3Д - сферы), постепенно расширяющиеся до границ ячеек.
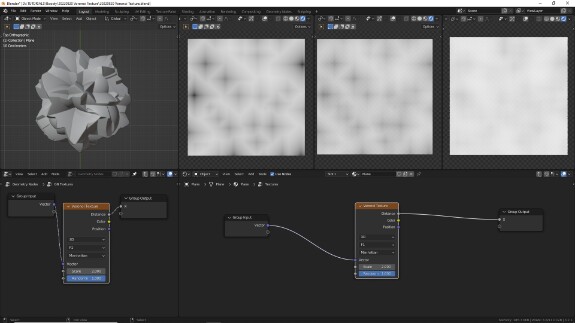
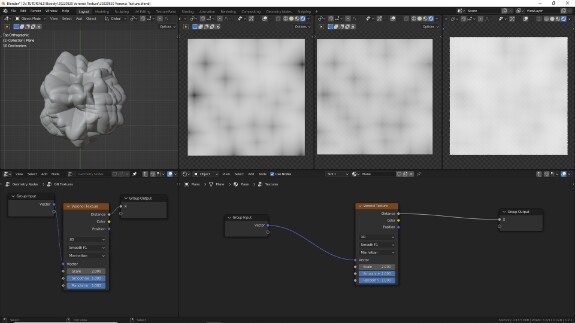
↑ F1 + Smooth F1, Manhattan. Внешний вид - ячейки с тёмной серединой и светлыми стенками. Форма - ромбы (в 3Д - октаэдры), постепенно расширяющиеся до границ ячеек.
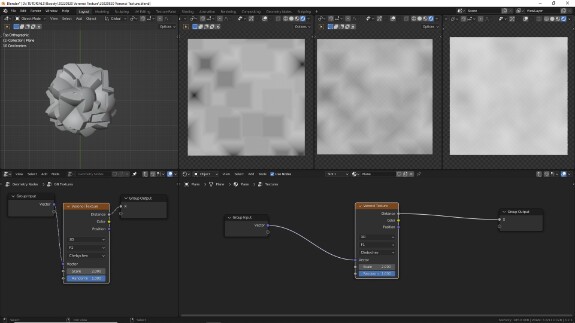
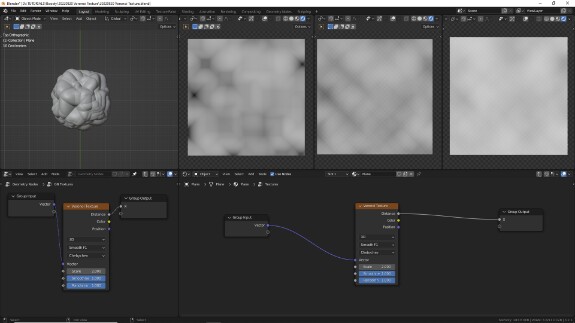
↑ F1 + Smooth F1, Chebychev. Внешний вид - ячейки с тёмной серединой и светлыми стенками. Форма - квадраты (в 3Д - кубы), постепенно расширяющиеся до границ ячеек.
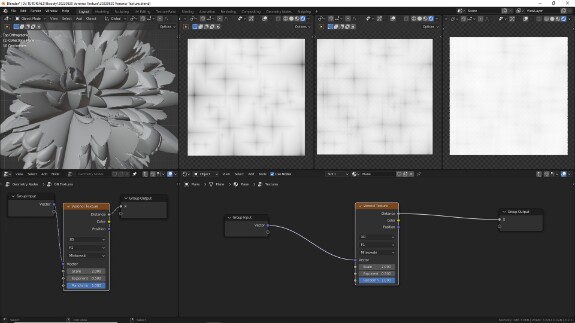
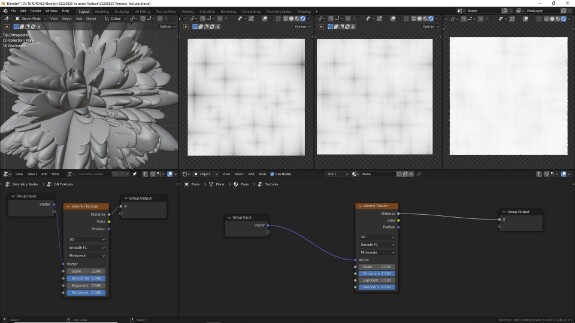
↑ F1 + Smooth F1, Minkowski. Внешний вид - ячейки с тёмной серединой и светлыми стенками. Форма - варьируется, в зависимости от значения Exponent.
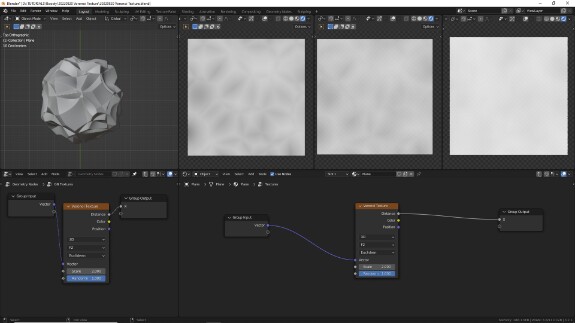
↑ F2, Euclidean. Рандомно расположенные ломаные кристаллы со светлой серединой, темнеющие к границам.
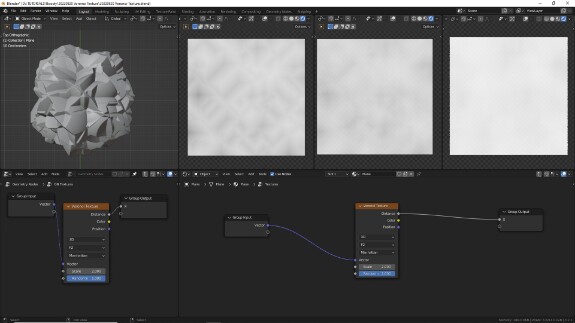
↑ F2, Manhatten. Расположенные по диагоналям разноразмерные прямоугольники (в 3Д - параллелепипеды).
↑ F2, Chebychev. Расположенные, согласно направлениям осей, разноразмерные прямоугольники (в 3Д - параллелепипеды).
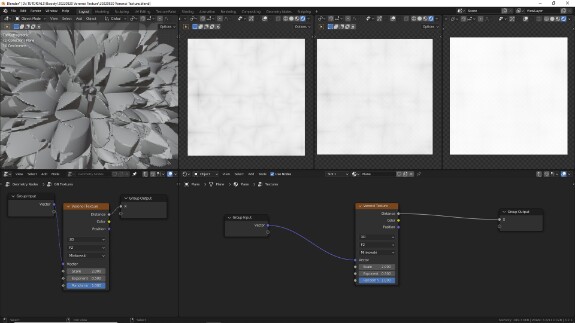
↑ F2, Minkowski. С Exponent по умолчанию выставленном на 0.5 - четырёхконечные (в 3Д - шестиконечные) "звёзды" с лучами, вытянутыми вдоль осей. Если смотреть с другой, технически более правильной стороны, где тёмный цвет обозначает не центр, а границы ячеек - то это квадраты (в 3Д - кубы) со скруглёнными краями. С изменением Exponent форма меняется.
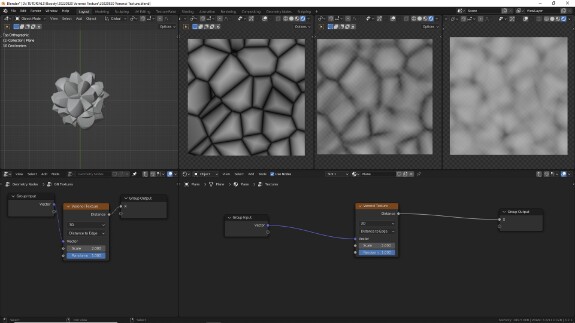
↑ Distance to Edge даёт чёткую, наименее размытую геометрическую структуру, внешне напоминающую потрескавшуюся землю в пустыне. Если после него использовать жёсткие ограничители типа Greater Than и Less Than, в отличие от других режимов явные геометрические фигуры будут проявляться не в центрах ячеек, а ими будут их границы. Это позволяет создавать структуры с тонкими линиями, особенно если искажать входящие векторные координаты с помощью техники Vector Noise, которую мы уже рассматривали в прошлых уроках и, я уверен, будем рассматривать не раз в последующих.
И напоследок несколько идей применения Voronoi Texture на практике, в сочетании с другими нодами. А в конце - самое важное.
Самое важное. Не забудьте рассказать об этом уроке друзьями, знакомым, в сообществах, пабликах, чатах, коммьюнити, в которых вы участвуете, себе на стенки в соцсети забирайте, чтобы не потерять. Лайки, комменты - всё это тоже помогает привлечь внимание других людей. Серьёзно. Хороший же контент, как-то хочется его донести до широкой аудитории.
blender
b3d
блендер
математика
материалы
шейдеры
математика в 3д
geometry nodes
текстуры
voronoi texture
Andrey Sokolov
Artistealer, в службе поддержки мне ответили, что вам нужно самостоятельно к ним обратиться. Это можно сделать, если прокрутить страницу до конца вниз, там есть кнопка "поддержка".
Илья Самусенко
Немного не понял RGB линии в эвклиде: когда я добавляю точку влияния 1 - я добавляю сетку с "ядрами". Когда добавляю вторую - то я добавляю еще одну внутрь предыдущей вокруг первого ядра? и так далее?
Илья СамусенкоReplying to Andrey Sokolov
Andrey Sokolov, я пытался повторить) но никак
Andrey SokolovReplying to Илья Самусенко
Илья Самусенко, в кривых вручную можно значения точкам по x и y вбивать, часто без этого прямо никак.
Артём Андреев
Андрей, просто потрясающие уроки, каждый как маленькое откровение!
Скажите пожалуйста, нет ли у вас в планах урока по созданию различных эффектов (погодных, например) процедурными шумами с целью оптимизации проекта? А то использование частиц сильно нагружает проект.
Скажите пожалуйста, нет ли у вас в планах урока по созданию различных эффектов (погодных, например) процедурными шумами с целью оптимизации проекта? А то использование частиц сильно нагружает проект.
Andrey Sokolov
Артём Андреев, спасибо! Чётких планов в рамках серии у меня нет, кроме доделать обещанное с бликами линзы, но вполне возможно )
Максим Гончарук
Кажется я проникся, затягивает! Прям радостно когда осознаёшь, что что-то уже откладывается в голове. Спасибо за урок! 






