Математика в 3Д ► 04. Math и маски
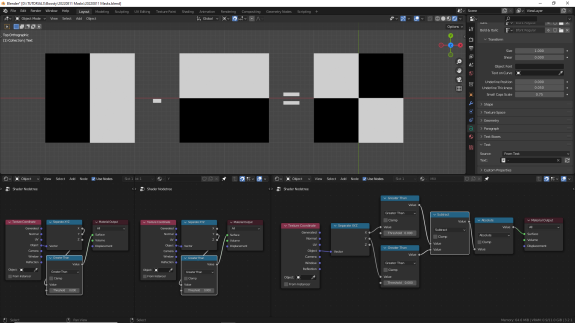
Текстурные координаты задают для каждой точки пространства уникальное значение. Я готов начинать с этого каждый урок. Поскольку эти значения числовые, мы можем проводить с ними математические операции.
В прошлом уроке мы работали с трёхмерными векторами, обрабатывая по 3 значения для XYZ одновременно. В этом подход будет немного изменён. Мы будем использовать одиночные числовые значения, взятые из двух разных координатных осей и представленные в виде чёрно-белых цветов, где чёрный - это числа от минус бесконечности до нуля, белый - единица, всё что между чёрным и белым - значения от 0 до 1, а всё, что белее белого - значения выше 1. Мы будем проводить между этим значениями простейшие математические операции - сложение, вычитание, умножение, деление и несколько видов сравнения с разным уровнем жёсткости - и смотреть, что будет получаться.
Буду очень благодарен всем, кто решит стать платными подписчиками или разово задонатить на означенные цели. Это сильно меня замотивирует на продолжение.
Больше всего нас будут интересовать области значений от 0 до 1, поскольку их можно использовать в качестве факторов смешивания цветов (с помощью нода Mix RGB) и шейдеров (с помощью нода Mix Shaders). Это и называется использовать маски, потому что в тех местах поверхности объектов, где на вход фактора смешивания будет приходить белый цвет (равный 1), будет использован цвет или материал из нижнего слота, а там, где чёрный (равный 0) - из верхнего:
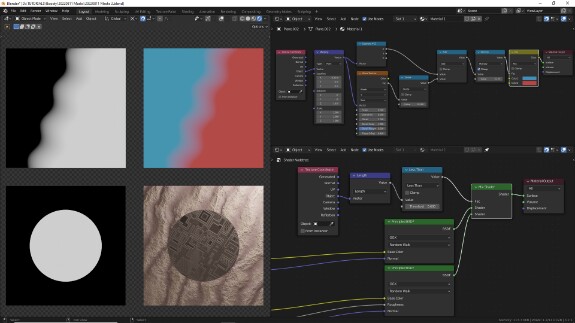
Диапазон от 0 до 1 универсален и легко управляем: его при необходимости впоследствии можно сдвинуть с помощью простого сложения или вычитания, увеличить с помощью умножения или уменьшить с помощью деления, изменить огибающую в нём с помощью возведения в степень, нодов ColorRamp, Map Range или RGB Curves.
Итак, мы возьмём две области значений - по оси Х и по оси Y, представленные в виде градиентов, и будем проводить над ними математические операции с помощью разных режимов нода Math. Нас будет интересовать в первую очередь, как это визуально отразится на цветах.
⚠ Обратите внимание! ⚠
Всё забываю об этом сказать. Если вы не повторяете всё, что я показываю, сами, своими руками в Блендер, эффективность этих уроков падает до 2-3%. Вы уже через неделю не сможете ничего вспомнить, так устроен человеческий мозг. Идеальное прохождение - один раз прочитать (опционально - законспектировать что сочтёте нужным). Один раз прочитать, повторяя пошагово. Несколько раз повторить самостоятельно, подсматривая то, что будет забываться. Последний шаг повторить на следующий день, потом через день перерыва и через неделю. И потом повторять периодически по мере необходимости, первые полгода хотя бы раз в месяц.
СЛОЖЕНИЕ (Add)
При сложении полностью белого и полностью чёрного цветов белыми остаются те части, которые были белыми хотя бы в одном из диапазонов. В данном случае чёрным (равным 0) остаётся только левый нижний квадрат, поскольку там ни в одном из диапазонов не было белого цвета (равного 1). Правый верхний квадрат белее белого, поскольку в обоих диапазонах там была единица, а при сложении получилась двойка.
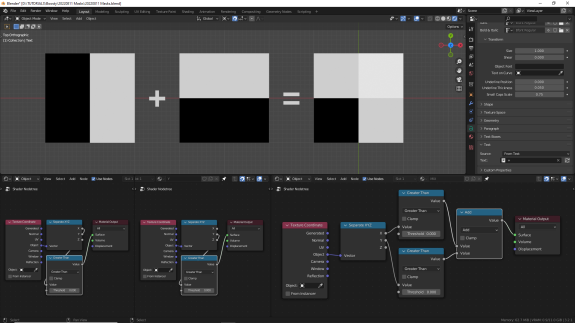
В этом примере используются ноды Math в режиме Greater Than, который все значения ниже значения Threshold делают чёрными (равными 0), а все выше Threshold - белыми (равными 1).
⚠ Обратите внимание! ⚠
При использовании черно-белых цветов в качестве масок, чтобы маски работали без ошибок, цвета следует удерживать в диапазоне от 0 до 1. Это можно сделать, поставив в результирующем ноде галочку Clamp. Тогда всё, что выше 1, будет приравнено к 1, а всё, что ниже 0 - к 0.
При сложении промежуточных, дробных значений результат визуально будет отличаться. Имейте в виду, что в данном случае, в отличие от предыдущего, где был использован диапазон от 0 до 1, используются также и минусовые значения осей координат: до -1 по осям Х и Y. Чтобы понять, почему получается диагональ, посмотрите внимательно на исходный и конечный результаты и проанализируйте, какие значения с какими складывались ↓
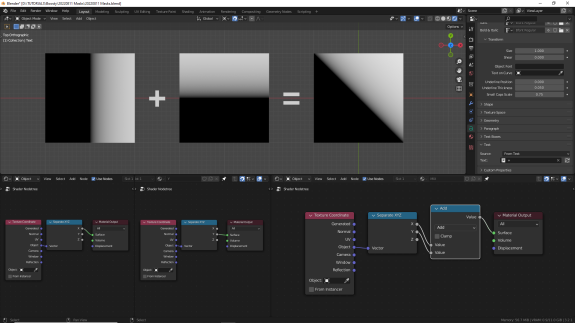
Обратите внимание, что чёрный - это не только 0, но и все значения ниже 0. Если поставить после результата нод Math в режиме Absolute, чтобы все отрицательные значения стали положительными, можно увидеть, что происходит в минусовом диапазоне на самом деле ↓
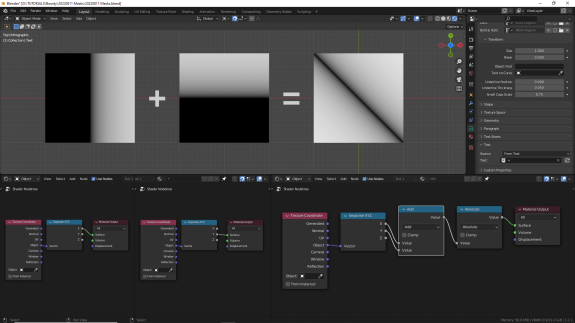
«Не видна взгляду тёмная сторона» (С) Учитель Йода.
Ну так вот, теперь видна.
Помните мы вначале ставили Greater Than ("больше, чем") до операции сложения? Если уже не помните, отмотайте чуть назад и посмотрите ещё раз на результат. Теперь поставим его после сложения (без Absolute). Результат будет сильно отличаться. Мы часто будем в дальнейшем использовать Greater Than для создания масок с жёсткими краями. С опытом вы научитесь интуитивно понимать, какого ожидать результата от тех или иных операций, но на начальных этапах стоит уделить время и приложить усилия к тому, чтобы проанализировать, что в каких случаях и почему получается математически ↓
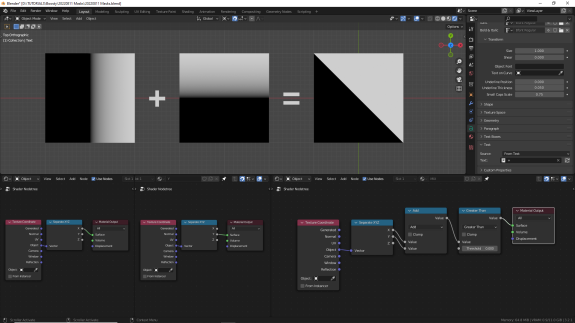
ВЫЧИТАНИЕ (Subtract)
При вычитании белыми остаются только те участки поверхности, которые в первом диапазоне были белыми, а во втором - чёрными. При вычитании, в отличие от сложения, порядок подключения к ноду Math важен ↓
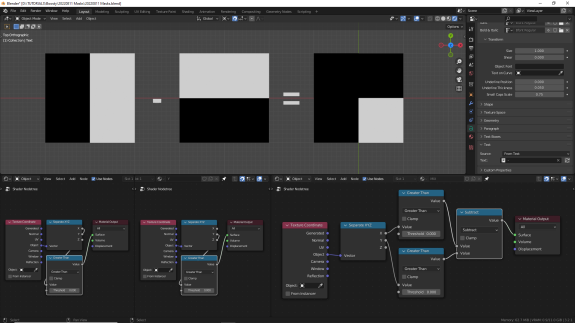
Имейте в виду, что при работе с вычитанием диапазонов от нуля до единицы могут образовываться отрицательные значения ↓
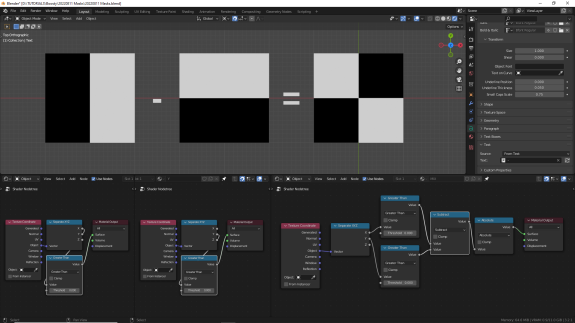
Опять же, при вычитании промежуточных, дробных значений результат визуально будет отличаться. Смотрим, анализируем, постигаем. Если ещё не пролистнули дальше, попытайтесь прикинуть, какие из значений окажутся в минусовом диапазоне ↓
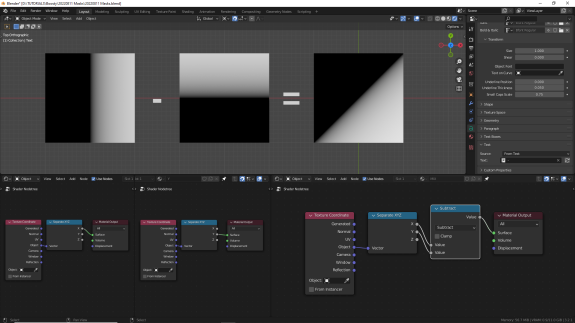
Ставим Absolute, проверяем значения в минусовом диапазоне ↓
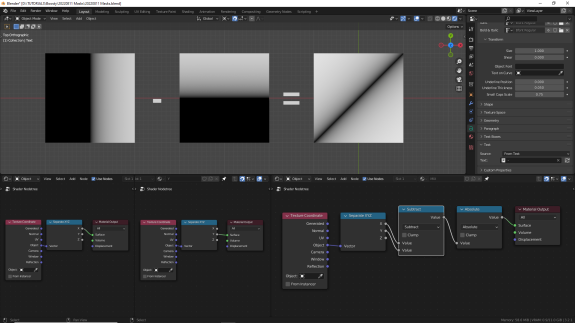
Ставим Greater Than, чтобы увидеть, как будет выглядеть жёсткая маска. Кстати, передвигая параметр Threshold, можно менять положение границы маски (попробуйте самостоятельно) ↓
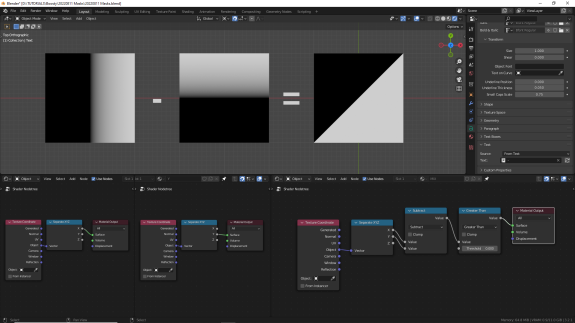
УМНОЖЕНИЕ (Multiply)
При умножении белыми остаются только те участки поверхности, которые были белыми и в том, и в другом объекте. Потому что чёрный - это 0, а при умножении на 0 любое число становится равным 0. Отрицательным значениям при умножении диапазонов от 0 до 1 возникнуть неоткуда ↓
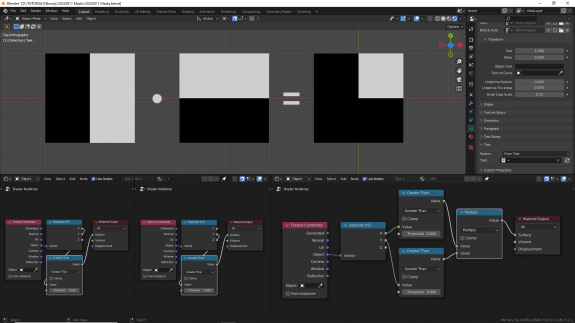
Поправка! Если вы перемножали диапазоны, в которых присутствуют отрицательные значения, то минус на минус даст плюс, и в том месте поверхности, где оба значения были отрицательными мы получим положительный результат (нижний левый квадрат). Упс, нежданчик! ↓
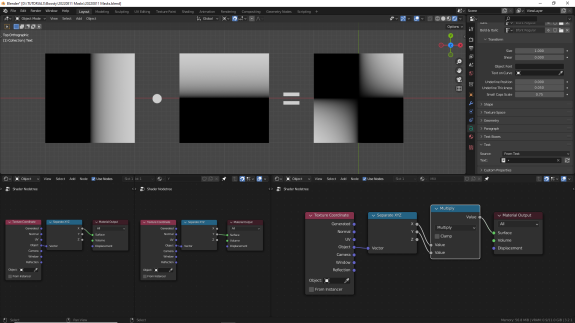
И, к слову, если уж речь зашла об отрицательных значениях, то плюс на минус даст минус. Ставим Absolute, чтобы в очередной раз убедиться, что не всё то, что чёрное - это ноль ↓
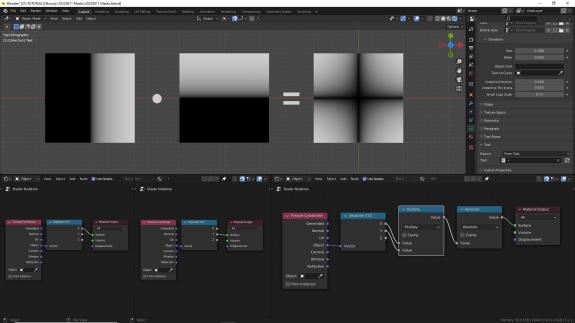
Поставим Greater Than, чтобы посмотреть, как будет вести себя жёсткая маска. А те, кто не ленится, и повторяет всё в Блендер, могут попробовать попытаться поднять Threshold. Я специально не стал показывать, что будет, чтобы не спойлерить, но если вы с этим ещё не сталкивались, результат может вас удивить! ↓
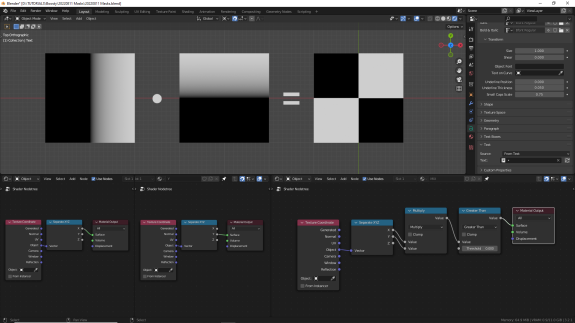
ДЕЛЕНИЕ (Divide)
Посмотрите на картинку ниже внимательно, и попытайтесь понять, что там не так. Прямо посчитайте по квадратам, начиная справа сверху, против часовой стрелки, что там должно получиться. Справа сверху мы делим 1/1 - получаем 1, всё ок. Слева сверху мы делим 0/1 получаем 0, всё ок. В правой нижней части мы делим 0/0... но на 0, как мы помним, делить нельзя. Поэтому, чтобы вселенная не сколлапсировала, а заодно чтобы не вылетать каждый раз с ошибкой, Блендер при делении любого числа на 0 возвращает в качестве результата 0. То есть если мы 0 делим на что-то - получаем 0 (чёрный цвет), и если мы что-то делим на 0 - получаем 0 (чёрный цвет). Таким образом, белыми опять остаются только те участки поверхности, которые были белыми и в том, и в другом объекте ↓
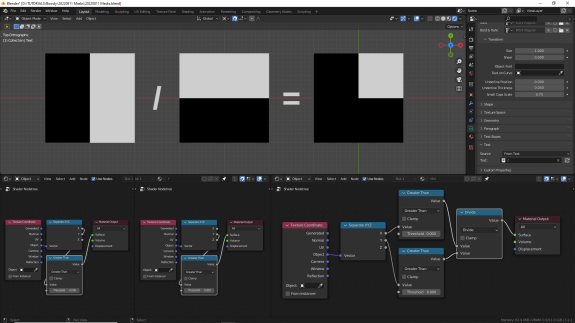
При делении дробных значений мы предсказуемо получаем на стыках результаты, стремящиеся к плюс и к минус бесконечности. Поэтому с делением всегда нужно внимательно проверять, что на что вы делите ↓
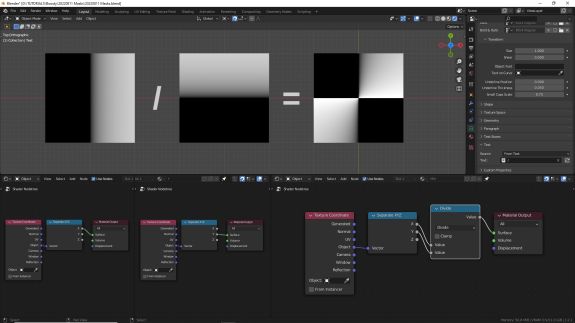
Ставим Absolute, чтобы проверить минусовой диапазон ↓
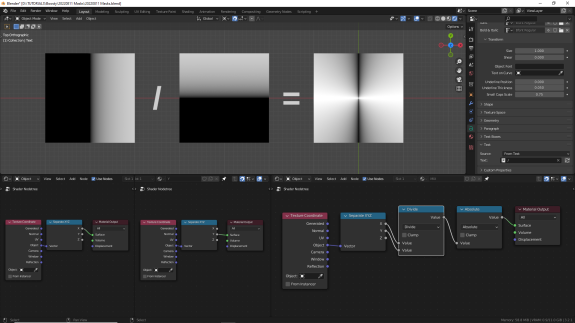
И ставим Greater Than, чтобы проверить, как работает жёсткая маска. Опять же сами смотрим, как срабатывает Threshold. Пытаемся понять, почему деление в этом случае даёт точно те же результаты, что и умножение. Если не получается, перечитываем параграф заново и пытаемся ещё раз ↓
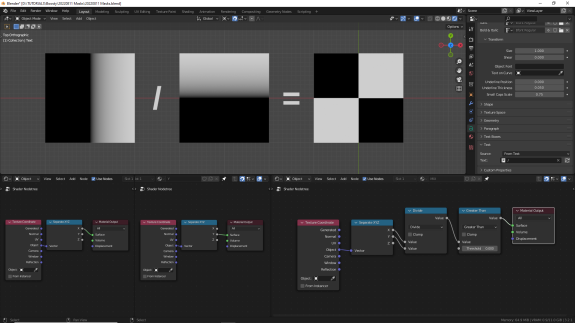
ОПЕРАТОРЫ СРАВНЕНИЯ
Далее мы будем сравнивать диапазоны между собой и смотреть визуальную репрезентацию результата. Для этого мы будем использовать следующие пары режимов нода Math с разным уровнем жёсткости:
• Самый жёсткий - Less Than (меньше чем) - Greater Than (больше чем)
• Помягче - Minimum (минимум) - Maximum (максимум)
• Самый мягкий - Smooth Minimum (мягкий минимум) - Smooth Maximum (мягкий максимум)
В общем случае они дают прямо противоположный результат, и, казалось бы, можно было бы использовать по одному режиму каждого уровня, а второй был бы просто инвертированным вариантом первого. Но поскольку, мы имеем дело, в том числе, и с отрицательными диапазонами значений, которые не всегда явно видны визуально, мне показалось, что не будет лишним показать эти режимы в парах (особенно с проверкой с помощью Absolute)
Greater Than/Less Than
В отличие от последующих режимов нода Math, эти режимы не возвращают исходные значения, результат всегда строго либо 0, либо 1. Для Less Than белыми остаются только те участки поверхности, значения которых в первом диапазоне меньше, чем во втором. Для Greater Than - наоборот.
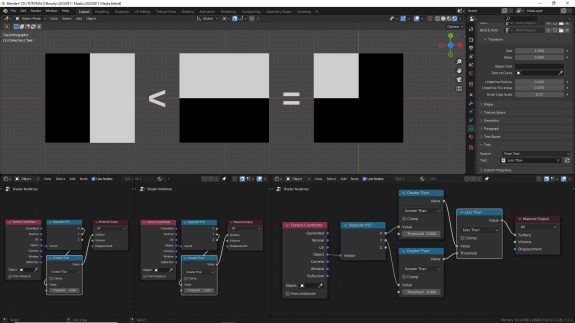
↑ Less Than
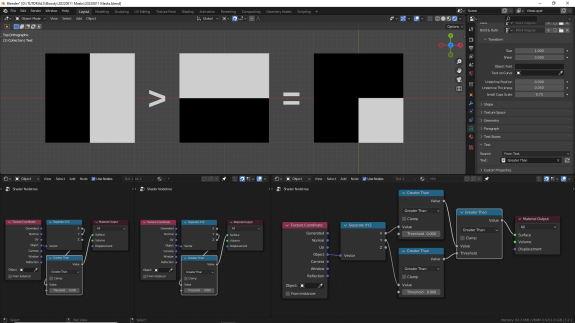
↑ Greater Than
При взаимодействии с дробными числами, опять же результат будет отличаться ↓
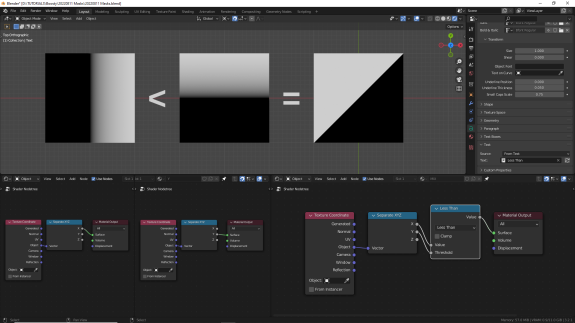
↑ Less Than
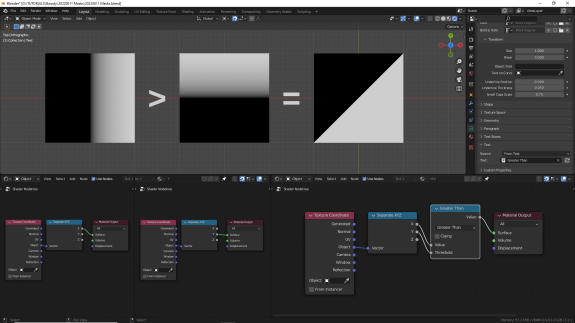
↑ Greater Than
Поскольку Greater Than и Less Than ВСЕГДА возвращают либо 0, либо 1, на отрицательные результаты мы их не проверяем.
Minimum/Smooth Minimum/Maximum/Smooth Maximum
Эти режимы нода Math возвращают, соответственно, наименьшее или наибольшее значение из двух диапазонов для каждой точки поверхности. Универсальных правил для них нет, просто будет возвращено либо меньшее, либо большее число. Режимы с приставкой Smooth отличаются только тем, что позволяют размыть границу срабатывания с помощью отдельного параметра. Для примера я установил этот параметр на значение равное Пи/2, просто потому что мы же тут математикой занимаемся, в конце концов.
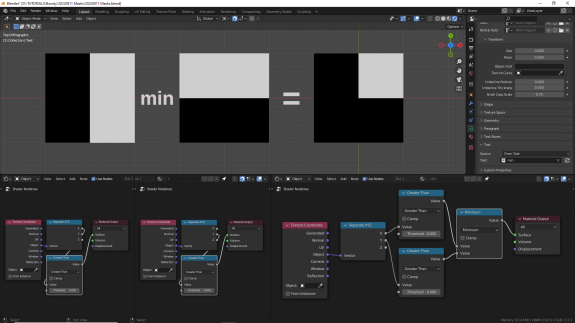
↑ Minimum
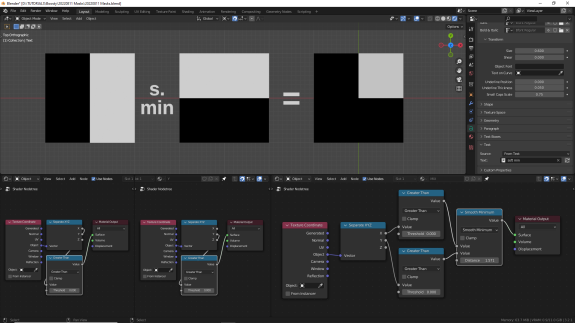
↑ Smooth Minimum
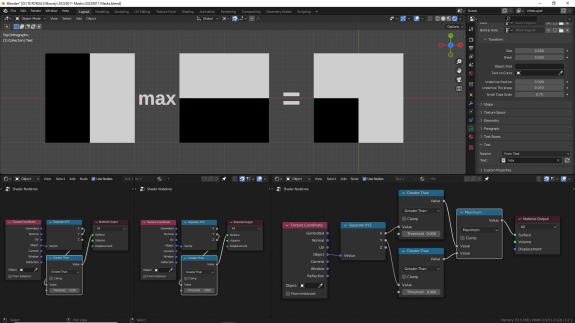
↑ Maximum
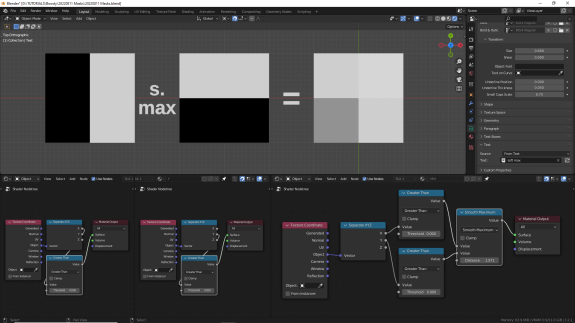
↑ Smooth Maximum
С дробными числами они также работают довольно предсказуемо, по крайней мере, для тех, что параллельно повторял всё в Блендер:
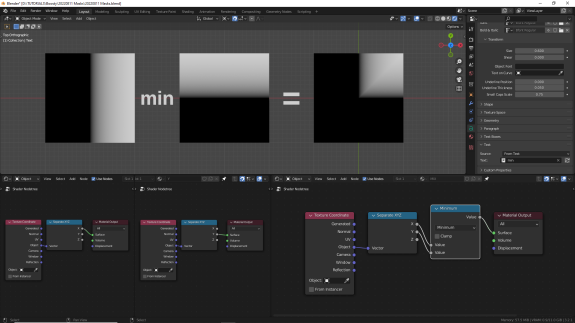
↑ Minimum
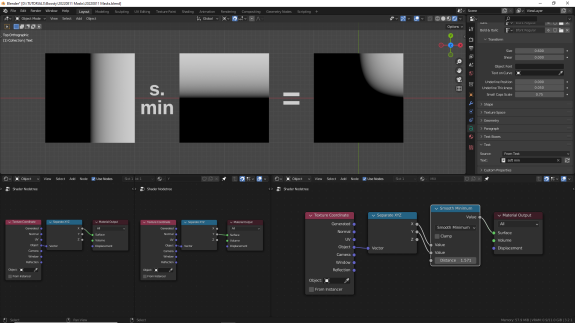
↑ Smooth Minimum
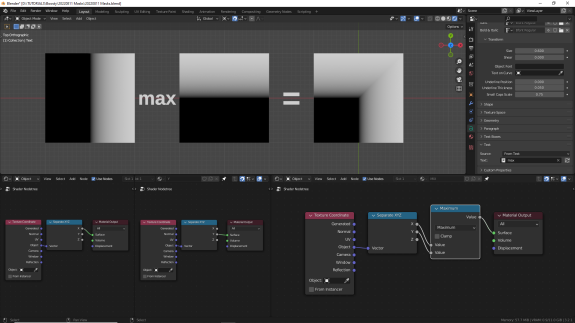
↑ Maximum
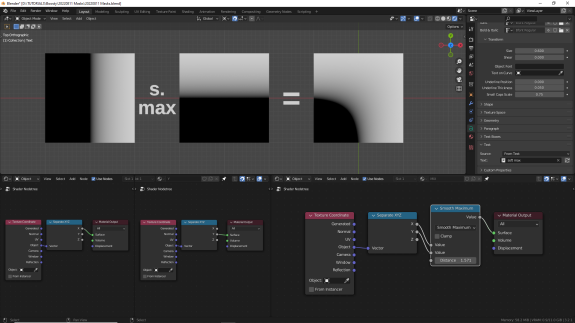
↑ Smooth Maximum
Поскольку мы работаем с диапазонами, в которых есть минусовые значения, помним, что часть результатов - это тоже не ноль а минус. Проверяем с Absolute:
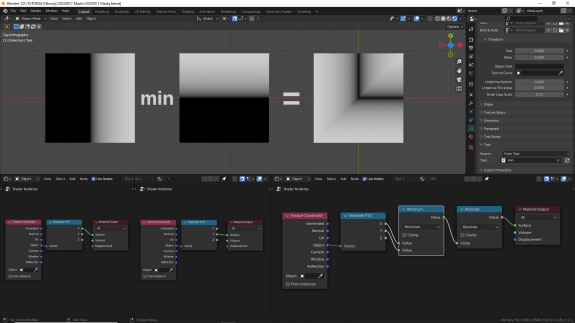
↑ Minimum
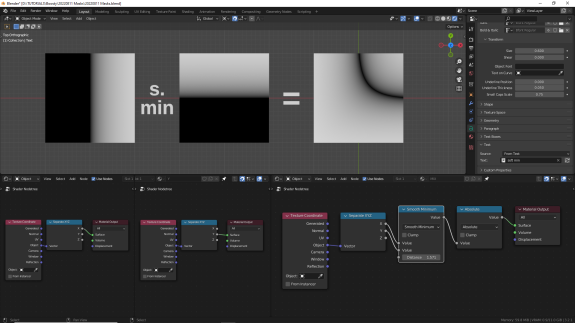
↑ Smooth Minimum
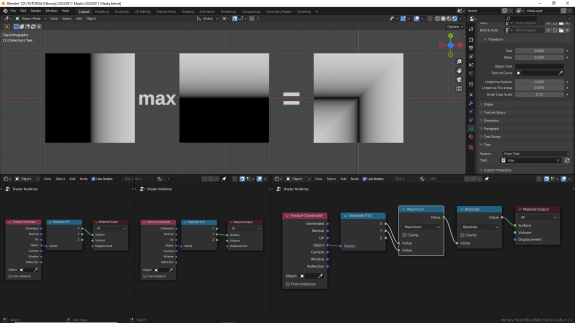
↑ Maximum
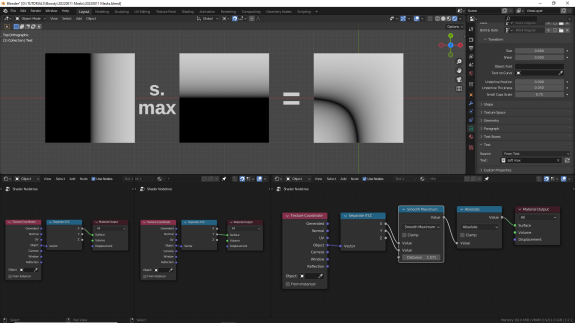
↑ Smooth Maximum
И смотрим, как они будут выглядеть с жёсткими масками. Обратите внимание, что хотя при нулевом Threshold Minimum выглядит так же, как выглядел Multiply, при добавлении Threshold результат будет совершенно другим.
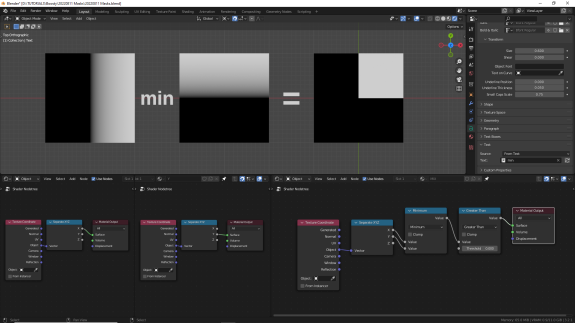
↑ Minimum
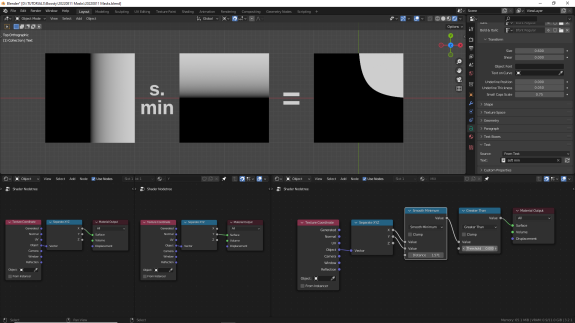
↑ Smooth Minimum
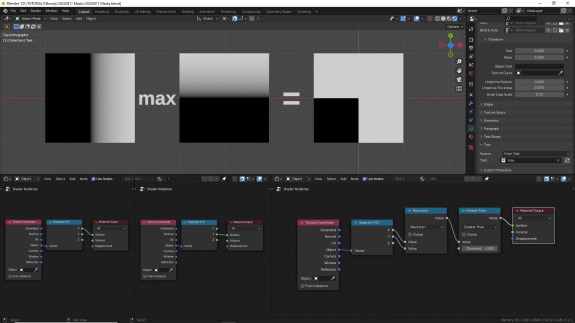
↑ Maximum
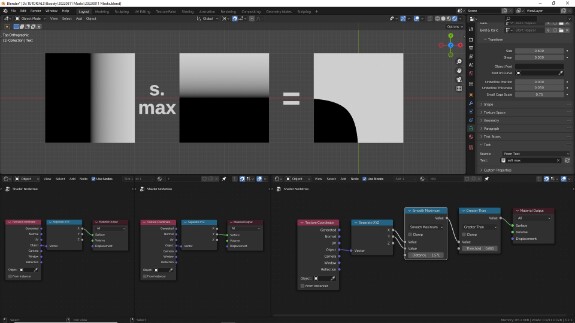
↑ Smooth Maximum
Пожалуйста, не забывайте оценить сам урок, ставить лайки публикациям с ним в соцсетях, писать комментарии, пускай даже несущественные, и делиться этими уроками у себя на страничках, в сообществах, пабликах, комнатах и чатах. Любая ваша активность помогает развитию проекта.





