Математика в 3Д ► 03. Векторные операции с текстурными координатами
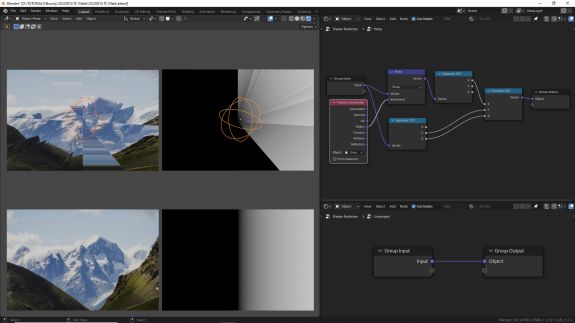
Математические операции с текстурными координатами влияют как на визуальную репрезентацию отдельных осей, так и на то, каким образом будет деформироваться текстура, для которой они используются.
Для векторных операций мы будем использовать разные режимы нода Vector Math, иногда - в сочетании с другими вспомогательными нодами, иногда - в сочетании с текстурными координатами других вспомогательных объектов.
На изображениях сверху будет изменённый результат, снизу - исходное, необработанное изображение.
Буду очень благодарен всем, кто решит стать платными подписчиками или разово задонатить на означенные цели. Это сильно меня замотивирует на продолжение.
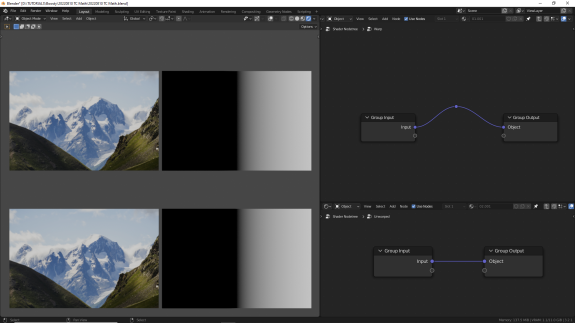
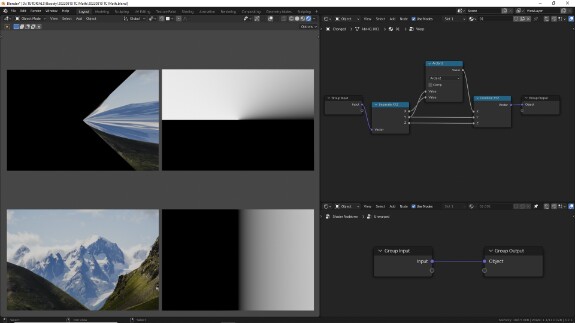
↑ Исходные текстурные коодинаты
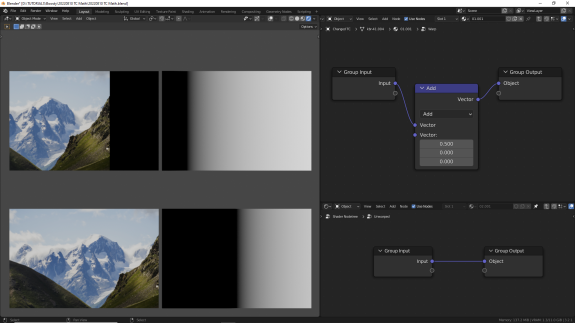
↑ Add - сложение, A+B. Сумма значений для каждой оси. Перемещает текстуру вдоль соответствующих осей.
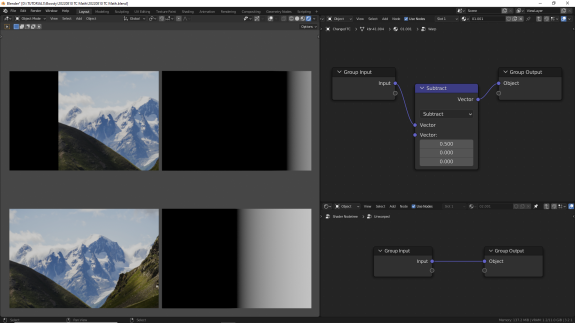
↑ Subtract - вычитание, А-B. Разность значений для каждой оси. Перемещает текстуру вдоль соответствующих осей.
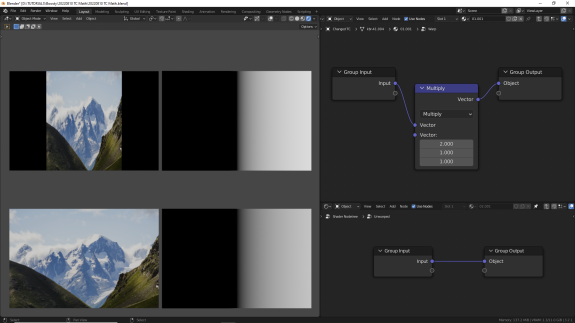
↑ Multiply - поэлементное умножение, А🞄B. Произведение значений для каждой оси. При значениях > 1 равномерно сжимает текстуру, при значениях от 0 до 1 равномерно растягивает текстуру, по соответствующим осям.
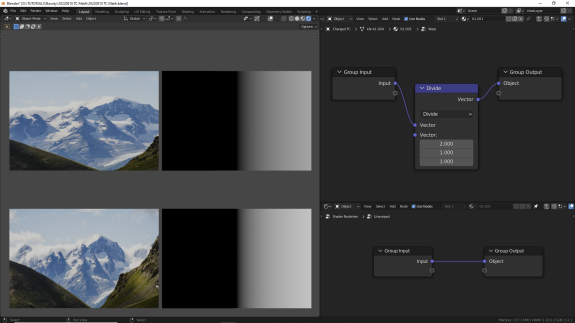
↑ Divide - поэлементное деление, А/B. Отношение значений для каждой оси. При значениях > 1 равномерно растягивает текстуру, при значениях от 0 до 1 равномерно сжимает текстуру, по соответствующим осям.
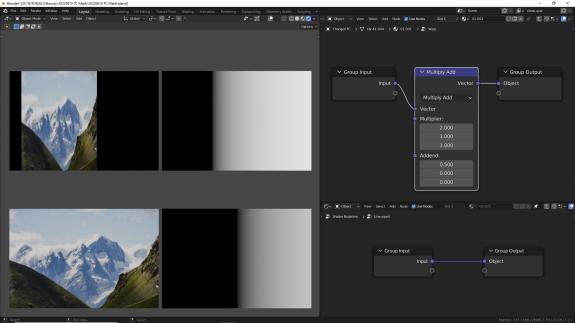
↑ Multiply Add - умножение и сложение, А🞄B+С. Произведение значений и последующая сумма со значениями третьего вектора для каждой оси. То же самое, что сначала произвести операцию Multiply, а потом Add.
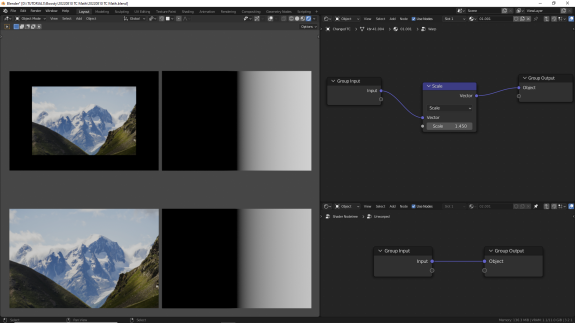
↑ Scale - умножение вектора на число. Равномерно сжимает или растягивает текстуру по всем трем осям
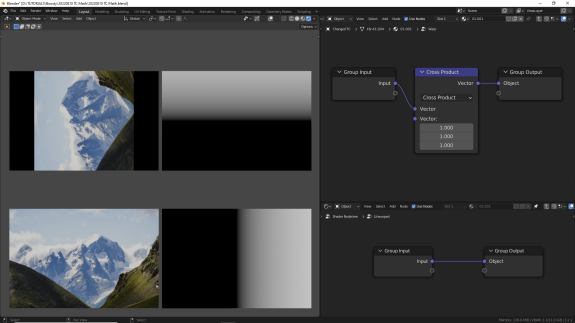
↑ Cross Product - векторное произведение, А×B. Возвращает вектор, перпендикулярный плоскости, образованной векторами A и B с длиной, равной площади параллелограмма, образованного векторами A и B. Разворачивает текстуру перпендикулярно двум входящим векторам
⚠ Очень важно для понимания! ⚠
Чтобы дальше понимать, что будет происходить, нужно понять, с какими именно векторами будут производиться операции. Велик риск начать ошибочно полагать, что Блендер использует в качестве векторов сами Текстурные Координаты - то есть мысленно рисует от начала системы координат стрелочки, равные одному метру, принимает их за вектор, каким мы его привыкли представлять визуально, и с этими "стрелочками" производит все эти операции. Это не так!
Да, вектор - это направленный отрезок, но поскольку для его определения нужны только его направление и длина, а не точное его расположение в пространстве, то вместо того, чтобы определять его 6-ю значениями - координатами по XYZ его начала и координатами по XYZ его конца, мы определяем его 3-мя значениями - только координатами по XYZ его конца, а начало вектора по умолчанию отсчитывается от (0, 0, 0) по XYZ.
То есть вот эти тройки значений в нодах - это координаты концов векторов, начала которых - всех векторов - лежат в точке (0, 0, 0).
И вот теперь, чтобы понять, что же именно высчитывает Блендер, нужно вспомнить, что значения в любых нодах - это не просто отдельные цифры, а что ноды в Блендер при просчётах присваивают эти числа из своих параметров каждой точке 3Д-пространства, и, соответственно, все вычисления проводятся для каждой точки 3Д пространства индивидуально - а не для каких-то "невидимых стрелочек".
То есть когда мы подаём на вход Vector Math текстурные координаты, которые, как мы помним из прошлых уроков, для каждой точки 3Д пространства задают свои значения, то фактически это означает, что в каждой точке пространства образуется свой индивидуальный вектор, определяющийся значениями по XYZ. И вот именно с этими индивидуальными векторами в каждой точке 3Д-пространства Блендер и проводит вычисления.
Это понятно? Тогда будет понятно и что происходит дальше при смешивании двух разных систем координат. Одна система координат для каждой точки пространства определяет одни значения, другая - другие, а нод Vector Math смотрит, чему в каждой точке равно значение той и другой системы координат, производит необходимые вычисления и определяет для этой точки новое результирующее значение.
Точных математических формул для некоторых функций в документации не представлено, поэтом ограничусь просто переводом их описания
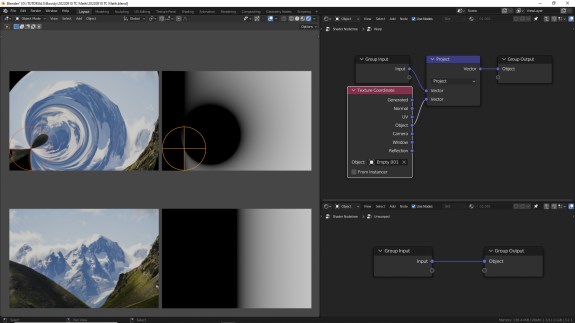
↑ Project - проекция вектора А на вектор B. В качестве вектора B я буду использовать системы координат Object объекта Empty (пустышки). То есть, получается, у нас в каждой точке пространства будут обрабатываться два набора по три значения, определяемых разными системами координат.
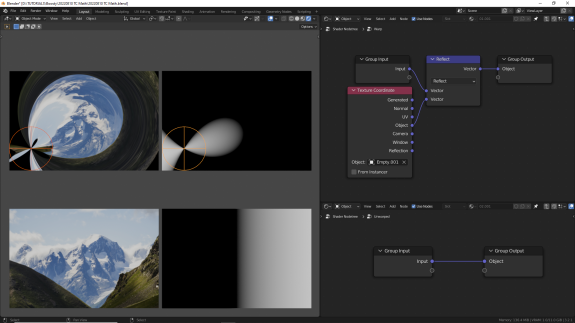
↑ Reflect - отражение вектора А вокруг нормали, представленной вектором B. Вектор B может быть не нормализованным (не приведённым по длине к единице).
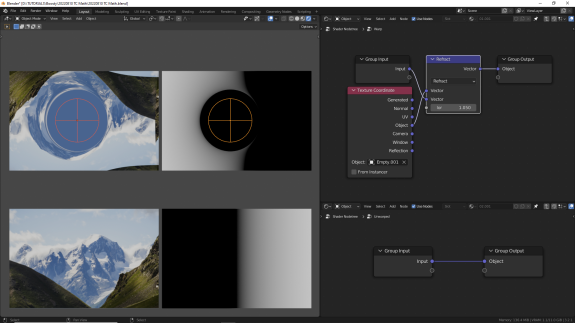
↑ Refract - для падающего вектора А, вектора нормали поверхности B и индекса рефракции (IOR) возвращает вектор рефракции (преломления).
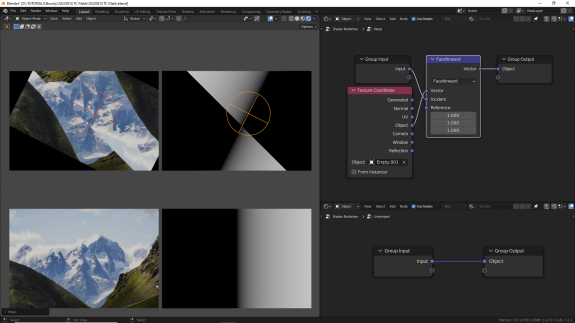
↑ Faceforward Ориентирует вектор А по направлению от поверхности B, определяемой нормалью C. Иными словами, если скалярное произведение (Dot Product) векторов B и C меньше 0 - возвращает вектор А, если больше или равно 0 возвращает вектор -А.
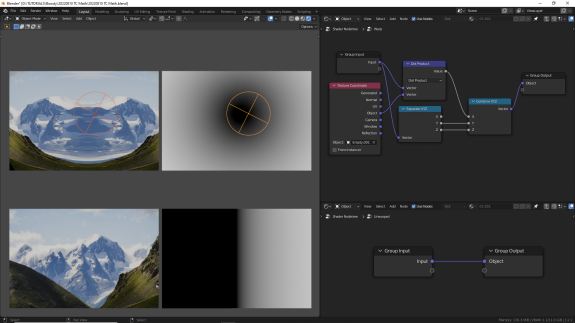
↑ Dot Product - скалярное произведение векторов. Произведение длин векторов А и В на косинус угла между ними. Поскольку Dot Product возвращает не вектор, а число (для каждой точки пространства, напомню), чтобы посмотреть, как он работает в качестве системы координат, мы будем его использовать только для оси X. Для этого с помощью нода Separate XYZ мы разделим исходный вектор на отдельные оси, ось Х заменим на обработанный результат, оси Y и Z оставим нетронутыми, и с помощью Combine XYZ соберём всё обратно в вектор.
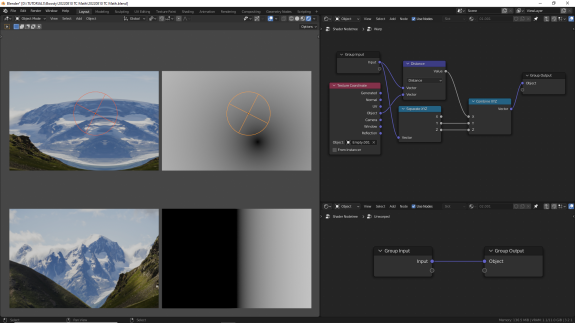
↑ Distance - расстояние между векторами A и B.
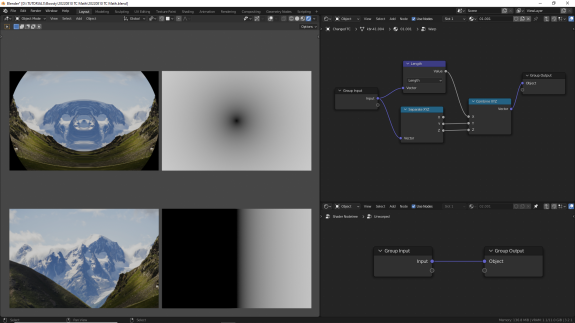
↑ Length - длина вектора. Она же квадратный корень скалярного произведения вектора самого на себя.
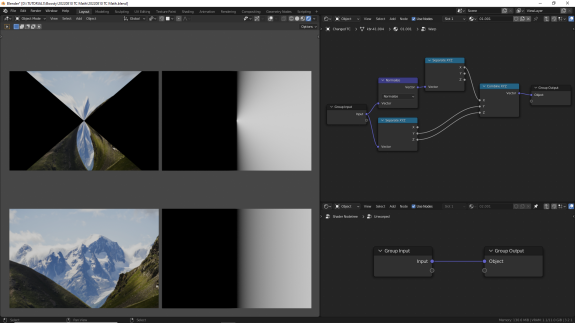
↑ Normalize - у результирующего вектора остаётся то же направление, что и у исходного, но длина вектора становится равной 1. Если вектор равен (0, 0, 0), результирующий вектор также равен (0, 0, 0).
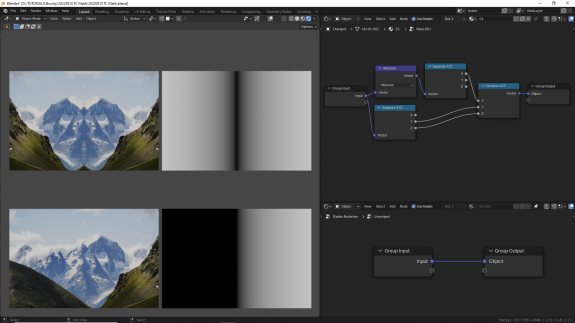
↑ Absolute - у всех отрицательных значений по каждой оси знак минус меняется на плюс.
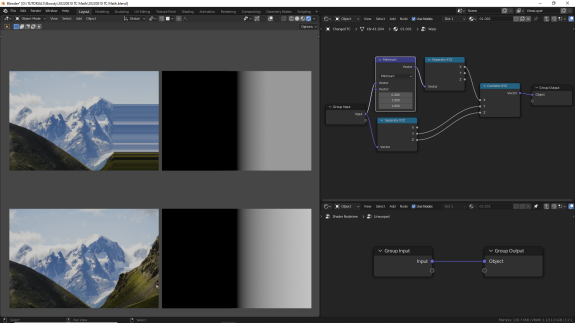
↑ Minimum - возвращает наименьшее значение из двух входящих по каждой оси
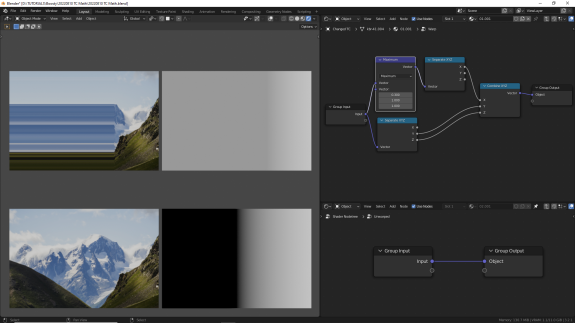
↑ Maximum - возвращает набольшее значение из двух входящих по каждой оси
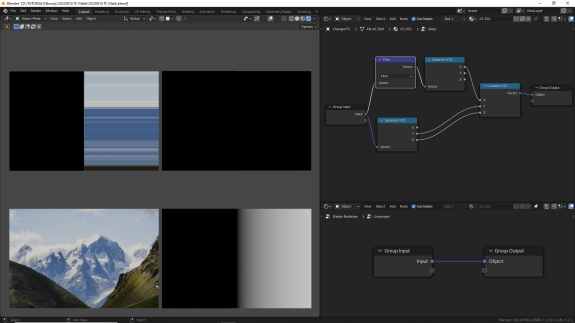
↑ Floor (нижнее пороговое значение) - возвращает новый вектор, элементами которого являются наибольшие целочисленные значения, которые меньше или равны элементам заданного вектора
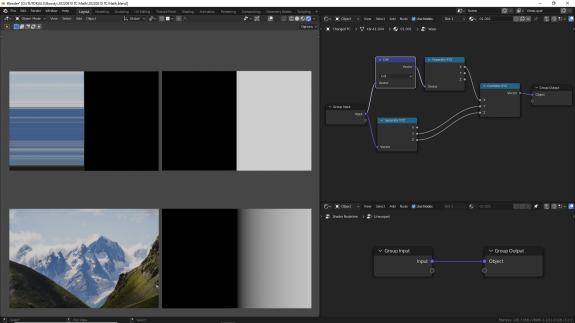
↑ Ceil (от ceiling, потолок) - возвращает новый вектор, элементами которого являются наименьшие целочисленные значения, которые больше или равны элементам заданного вектора.
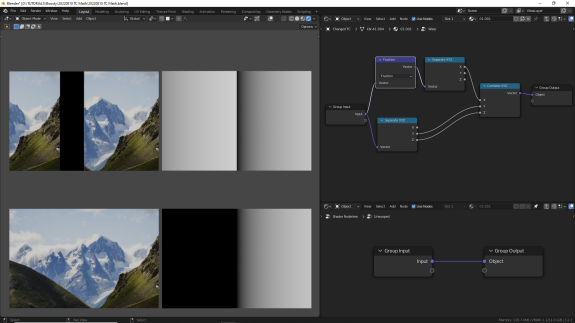
↑ Fraction (дроби) - возвращает дробные части значений для каждой оси. Таким образом, независимо от входящих значений, результат всегда будет в пределах от 0 до 1 (не включительно).
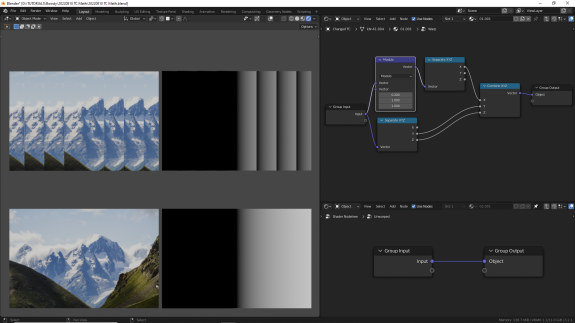
↑ Modulo (по модулю) - остаток от деления для каждой оси. Также всегда будет в пределах от 0 до 1 (не включительно).
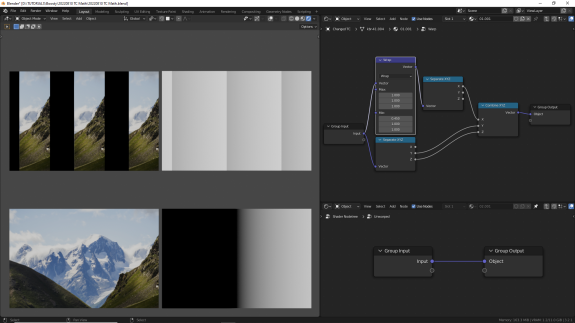
↑ Wrap (сворачивание/округление/упрощение). В документации просто ссылка на эту статью. Гугл-переводчик вам в помощь и Блендер для экспериментов в руки.
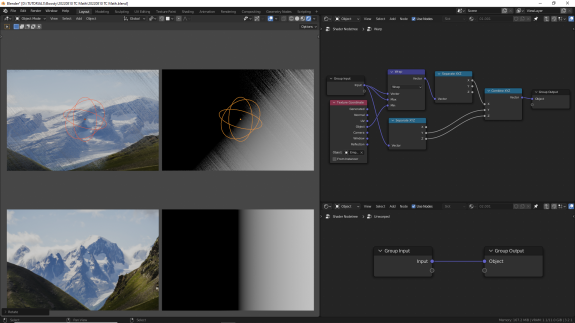
Я всё же не математик, но как сиджишник могу посоветовать попробовать вот такое использование Wrap для добавления глитчей ↑
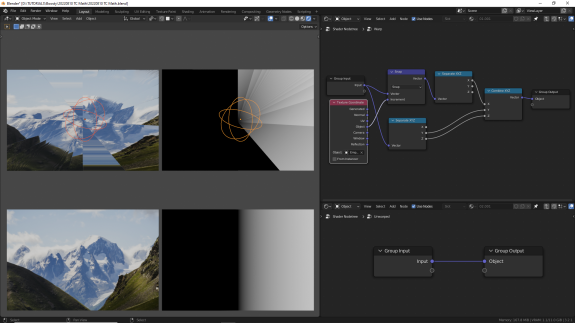
↑ Snap (привязка). Результат округления A до наибольшего целочисленного значения, кратного B, меньшего или равного A. (Что это вообще должно значить??? Но на практике может выглядеть прикольно!)
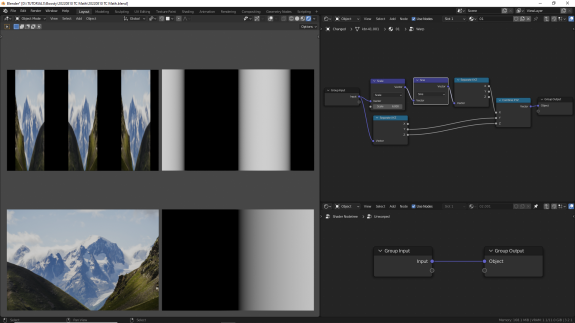
↑ Sine (синус). Ну, это пошла тригонометрия, с этим мы уже знакомы. Синус высчитывается для каждой оси индивидуально. Обратите внимание, что картинка попеременно развёрнута то в одну, то в другую сторону.
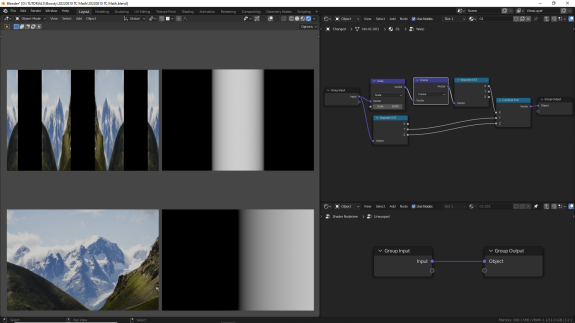
↑ Cosine (косинус). То же, что и синус, только со смещённой фазой (ну, это объяснение с поправкой на практическое применение, не вдаваясь в детали).
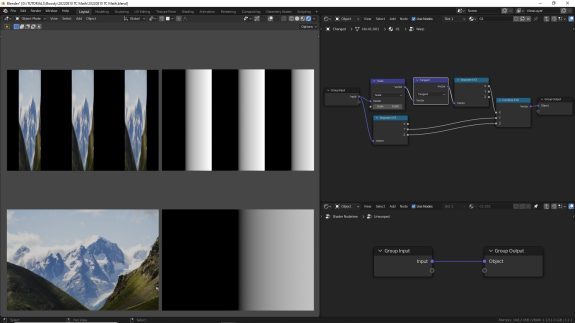
↑ Tangent (тангенс). В отличие от синуса и косинуса, у которых "волна" доходит до крайней верхней точки и потом медленно откатывается в обратном направлении, у тангенса после верхней точки происходит резкий скачок к нижней. Обратите внимание, что здесь картинка при дублировании уже смотрит в одну и ту же сторону. Также высчитывается индивидуально для каждой оси.
Помимо Vector Math, мы можем использовать для математических операций с отдельными осями и нод Math, что ещё больше расширяет возможности. Напоследок несколько примеров:
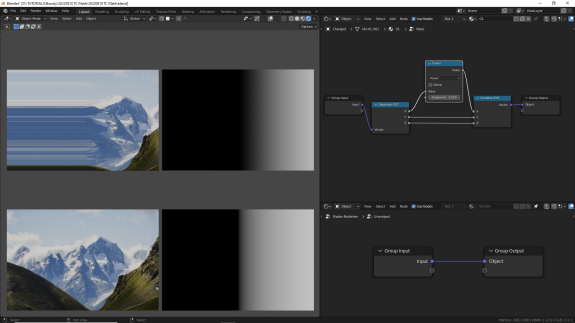
↑ Power - возведение значения в степень.
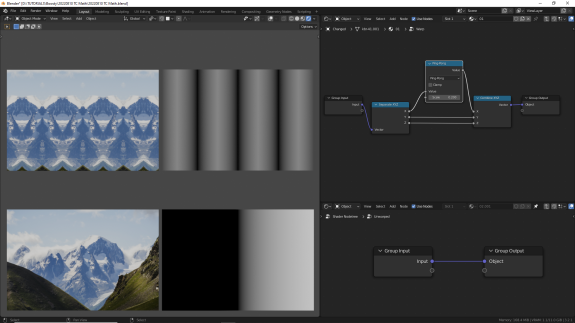
↑ Ping Pong - пинг-понг.
↑ Arctan2 - уже знакомый нам по первому уроку арктангенс с двумя входящими параметрами, с помощью которого можно делать лучи или оборачивать текстуру по кругу - но об этом речь пойдёт уже в следующих уроках.





