Математика в 3Д ► 10. Waves Texture

Если вы смогли разобраться, как работают Noise Texture и Musgrave Texture, то с пониманием того, как работает Waves Texture, у вас не должно возникнуть никаких проблем. А если вы начинали с самого первого урока, то не составит труда понять и математику, лежащую в её основе, тем более, что ничего сложного там нет. Это будет небольшой и несложный урок.

Буду очень благодарен всем, кто решит стать платными подписчиками или разово задонатить на означенные цели. Это сильно мотивирует на продолжение.

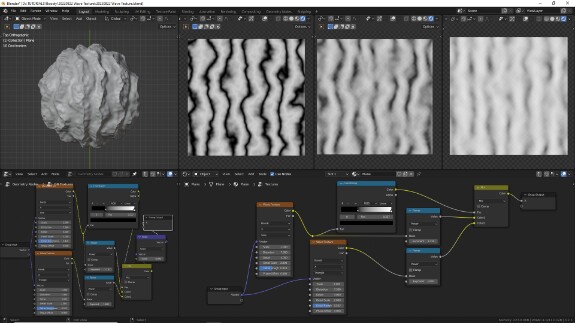
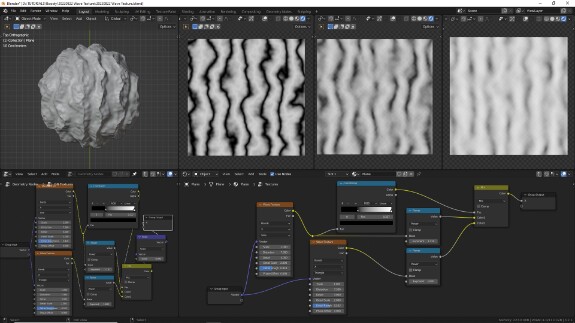
Как и в предыдущих уроках, используются текстурные координаты типа Object (в Geometry Nodes - Position). Слева направо показаны:

• Сдвиг вертексов относительно нормалей с помощью геометрических нодов

• Срез на плоскости

• 5 срезов, на небольшом расстоянии, наложенных друг на друга

• трёхмерный волюметрик материал

Подробнее про то, как настроен проект, здесь.

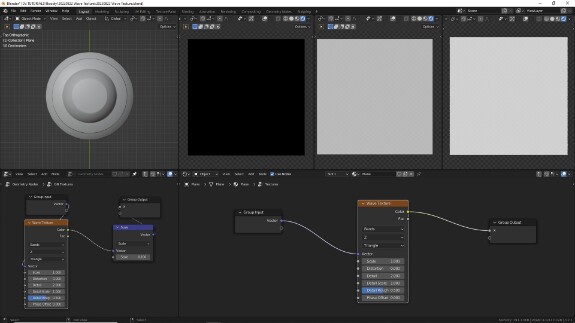
↑ Waves Texture с настройками по умолчанию. Waves переводится как Волны. И эта процедурная текстура, как следует из её названия, генерирует волны. А как вы можете помнить, волны по координатным осям генерируются с помощью синуса, косинуса или тангенса. Ниже я покажу, как именно.

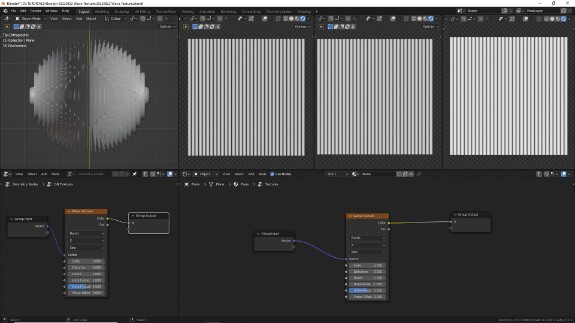
↑ Параметр Scale изменяет длину волны. Чем меньше Scale, тем более крупные будут волны

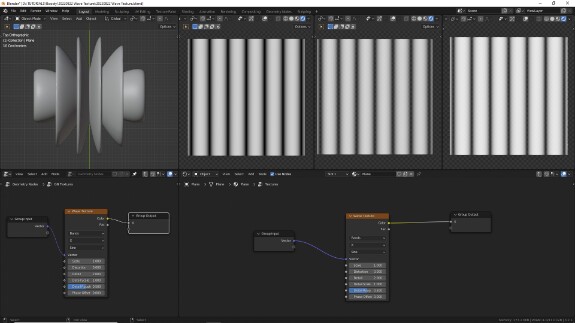
↑ Поскольку диапазон значений, генерируемых Waves Texture, равен от 0 до 1, для геометрии это означает, что в пиках она будет сдвигаться на 1 метр. Для визуализации это многовато, поэтому, чтобы лучше рассмотреть, какие формы принимает геометрия под воздействием Waves Texture, я решил сжать этот диапазон, и для этого добавил Vector Math в режиме Scale со значением 0.1.

🛈 Выход Color у Waves Texture жёлтого цвета, что означает в Blender цветовую информацию. Но в данном случае при передаче цвета используется линейное цветовое пространство (linear), а не стандартное sRGB, поэтому цветовая информация, получаемая на выходе, подаётся в нетрансформированном, нескорректированном виде, и мы можем использовать её числовые значения в качестве именно числовых значений, т.е. в качестве векторов для каждой точки пространства, и применять на них векторную математику, без опасений, что что-то может неверно интерпретироваться и искажаться. 

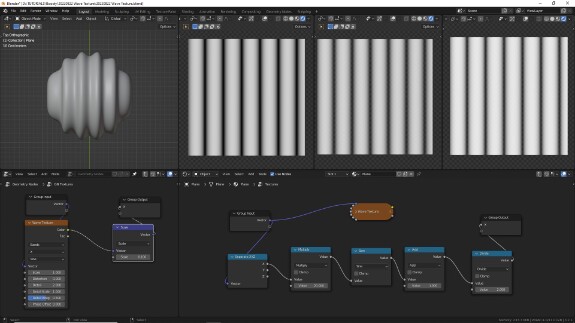
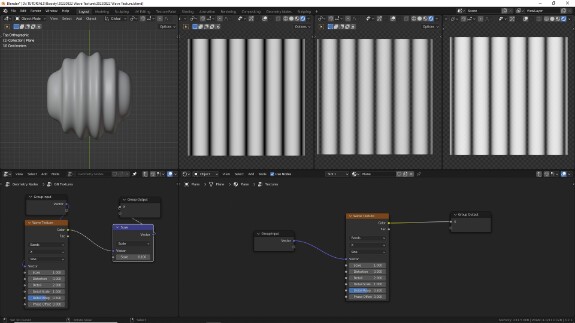
↑ Справа внизу в Shader Editor - приблизительная внутренняя математика, стоящая за генерацией волн. Берутся текстурные координаты по какой-нибудь из осей (Separate XYZ > X). Происходит корректирующее умножение с помощью Math в режиме Multiply (умножение). Можно добавить ещё один Math > Multiply, и он будет выступать в качестве параметра Scale. Полученный результат подаётся на вход синуса, Math > Sine, чтобы сгенерировать волны. Так как синус выдаёт значения в диапазоне от -1 до 1, то чтобы привести этот диапазон к от 0 до 1, сначала к нему добавляется с помощью Math > Add (сложение) 1 - получается диапазон от 0 до 2, а потом результат делится на 2 с помощью Math > Divide (деление). Результат получается аналогичный, с небольшим сдвигом фазы.

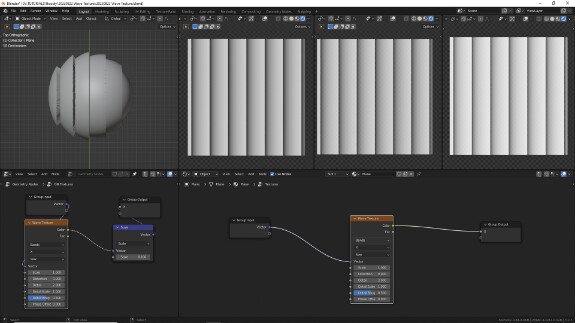
↑ Изменение типа Sine на Saw (в переводе - пила) даёт волны пилообразной формы, похожей на те, что производит тангенс: значения поднимаются от 0 до 1, но вместо того, чтобы плавно возвращаться обратно, по достижении 1 происходит резкий скачок обратно к 0, и всё повторяется заново.

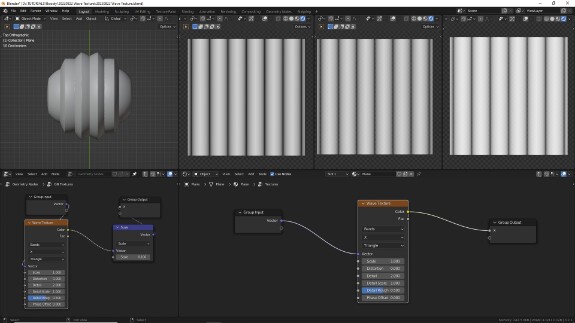
↑ Изменение этого параметра на Triangle даёт волны треугольной формы. Значения линейно поднимаются от 0 до 1 и линейно опускаются обратно.

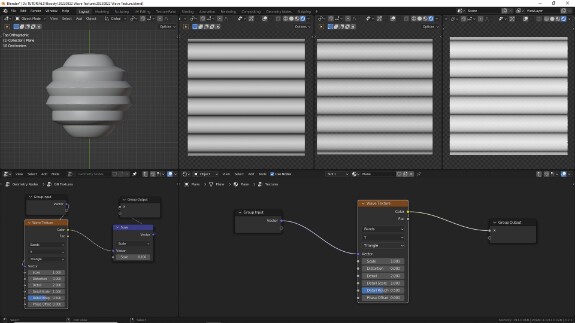
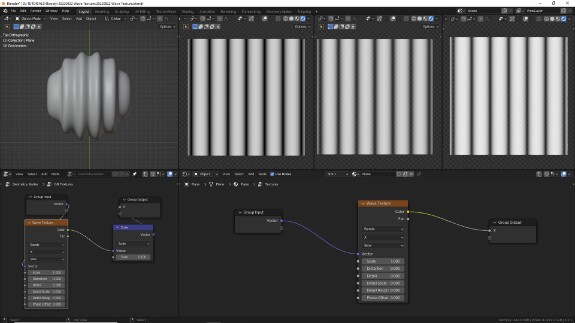
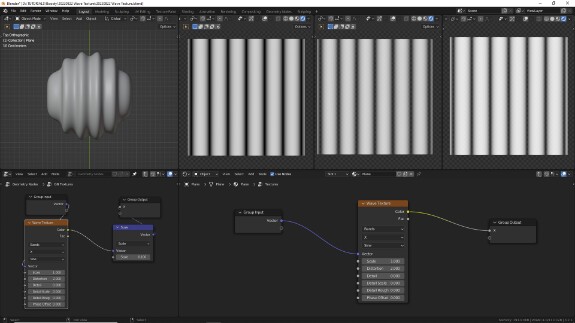
↑ Второй сверху параметр (по умолчанию X) определяет координатную ось, по которой генерируются волны. На скриншоте - распространение по оси Y.

↑ Обратите внимание, как распределяются волны, если смотреть прямо перпендикулярно на ось, по которой они распространяются, в данном случае Z.  На материалах видно, что в этом случае значения волны заливают собой всю плоскость. На плоском срезе цвет чёрный, потому что в этом месте волна оказывается в низшей точке, на нуле. Это не правило, просто в этом случае так сложилось. На нескольких срезах и в волюметрик материале значения волн суммируются

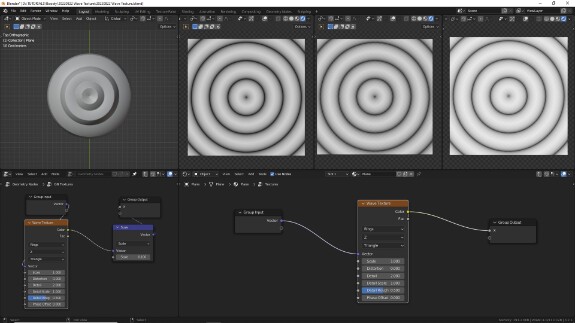
↑ У первого сверху параметра два варианта - Bands и Rings - то есть полосы и кольца. В режиме Rings мы получаем концентрически расходящиеся волны, образующие кольца. Те, кто проходил предыдущие уроки, могут догадаться, что такого эффекта можно добиться, если в качестве оси X использовать не саму ось, а длину расстояния от неё (например, Vector Math в режиме Length).

По режимам это всё. Ещё раз, сверху вниз, они определяют:
• Способ распространения волн

• Ось, по которой или вокруг которой (в зависимости от верхнего параметра) распространяются волны

• Форму волны

🛈 Разумеется, я не просто так показывал и объяснял математику, стоящую за генерацией волн. Как несложно догадаться, потенциально она даёт ключ к намного более точному контролю как над способами распространения волн, так и над их формой.

К параметрам, определяющих свойства самих волн, также относится самый нижний параметр Phase Offset. Забегая вперёд, он просто сдвигает волны вдоль оси, позволяя их анимировать. Упоминаю я его сейчас, потому что по сути он, как и режимы выше, определяет одно из базовых свойство волн - их положение. Остальные же числовые параметры (ну ещё кроме Scale) относятся уже к управлению искажениями волн, а не к их базовым свойствам. И вот их мы сейчас и рассмотрим.

↑ Для начала обнулим все числовые параметры (выставим все значения на 0), чтобы рассматривать их по отдельности, в чистом виде. А в конце я покажу, что за ними стоит, и логика их работы сразу станет простой и понятной, потому что с этой техникой мы уже сталкивались раньше.

↑ Параметр Distortion (искажения) должен искажать волны. Однако, если его добавить, пока все параметры ниже равны 0, ничего не произойдёт. Поскольку эти параметры называются так же, как и в Noise Texture, логично было бы предположить, что они и работать должны так же: Distortion должен бы искажать конечный результат в любом случае, а его размер - зависеть от значения Scale, Detail - контролировать добавление уровней детализации, Detail Scale определять размер уровней детализации, а Detail Roughness - объём подмешивания мелких уровней детализации. Но это не так! Точнее, не совсем так.

Для искажения волн действительно используется тот же паттерн, что и в Noise Texture. Настройки Detail и Detail Roughness - напрямую взяты из Noise Texture. Но параметр Distortion и Detail Scale работают не так, как можно было бы подумать.

Distortion в действительности отвечает за общий объём добавляемых к волнам искажений, а не за их "завихрения", как в Noise Texture. То есть Distortion - это то, насколько сильными будут искажения. Но чтобы сами искажения появились, необходимо добавить параметр Detail Scale.

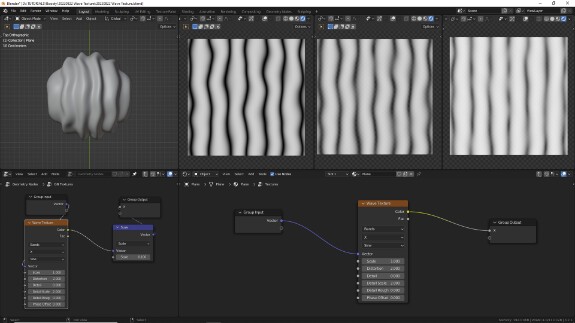
↑ Параметр Detail Scale в Waves Texture выполняет ту же функцию, которую в Noise Texture выполняет параметр Scale. То есть отвечает за базовый размер паттерна шума, лежащего в основе искажений. Поэтому, чтобы искажения начали появляться, он должен отличаться от 0. Тогда с помощью Distortion можно будет регулировать, с какой силой будут добавляться эти искажения.

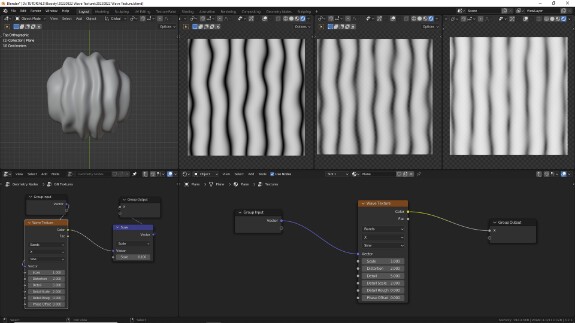
↑ Параметр Detail, как уже отмечалось, работает как и в Noise Texture - отвечает за количество добавляемых уменьшенных копий паттерна шума, накладывающихся друг на друга.

🛈 Подробно идея фрактального шума и процесс наложения копий паттерна описан в уроке про Musgrave Texture.

Как и в Noise Texture, пока параметр Detail Roughness равен 0, добавление Detail никакого результата не даст, потому что Detail Roughness отвечает за то, в каком объёме к основному паттерну будут подмешиваться его уменьшенные копии, которые мы определяем с помощью Detail.

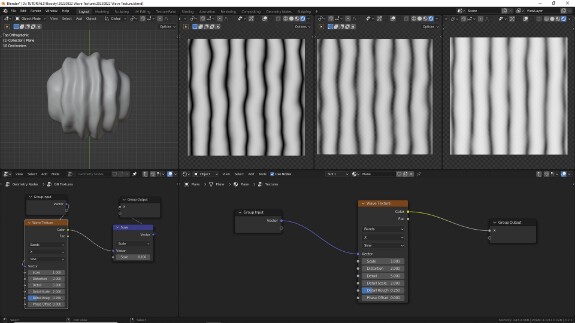
↑ С добавлением Detail Roughness уменьшенные копии паттерна шума, количество которых определяется параметром Detail, постепенно начинают подмешиваться к основному паттерну шума, размер которого, напомню, определяется параметром Detail Scale.

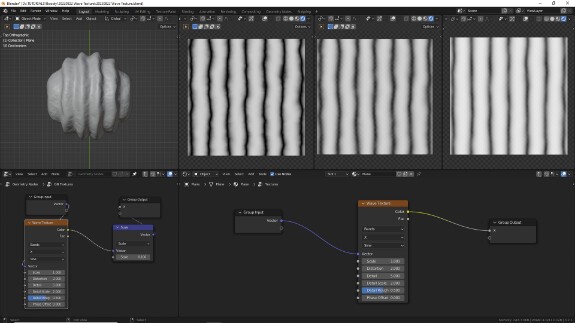
↑ Чем больше Detail Roughness, тем больше ощущается влияние параметра Detail.

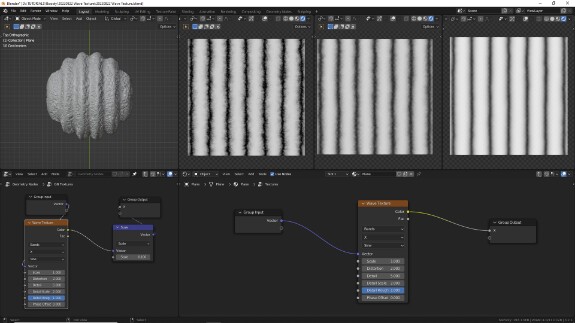
↑ Когда Detail Roughness достигает 1, влияние Detail становится максимальным.

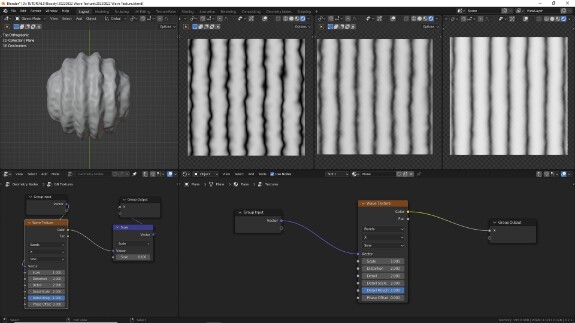
↑ Не думаю, что на практике Detail Roughness часто используется на максимальном уровне в художественных целях, но выкрутить его на полную, чтобы точнее отстроить параметр Detail - хорошая идея.

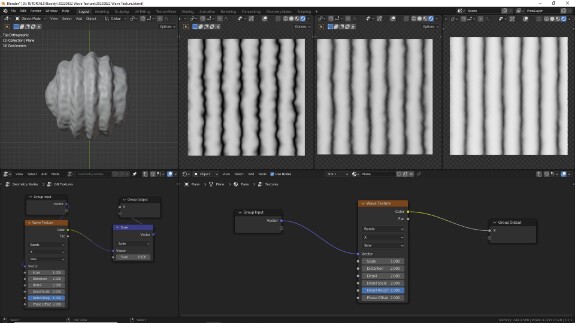
↑ Как уже было отмечено выше, Phase Offset не имеет отношения к детализации и просто сдвигает волны вдоль оси. Обратите внимание, что координаты паттерна шума, отвечающего за искажения, при этом остаются на месте, и получается, что волны как бы проходят через искажения, что придаёт им больше естественности во время анимации.

Если вам нужно сдвигать искажения вместе с волнами, просто поставьте перед векторным входом в Waves Texture нод Vector Math в режиме Add и в нём добавляйте значения по нужной оси. Кстати если изменяемая в Vector Math ось будет отличаться от выставленной в самой Waves Texture, это может дать интересные эффекты, когда основные крупные волны будут оставаться на месте, а искажения будут проходить сквозь них.

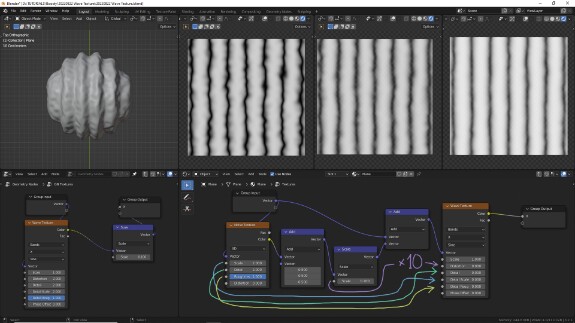
↑ И напоследок, как и было обещано - демонстрация того, что происходит за кадром в Waves Texture. Как можно было догадаться, это уже известная нам техника векторного шума. Не буду комментировать, попробуйте разобраться сами, мы всё это уже проходили, это не должно быть сложно.

↑ Пример сочетания двух Waves Texture с разными настройками - нижняя часть "волн" пологая, а верхняя - острая

Если вам нравятся эти уроки, поблагодарите, пожалуйста, хотя бы мысленно, тех, кто забирает их к себе на стенки, рассказывает о них друзьям, знакомым, в сообществах, пабликах, чатах, коммьюнити. Этих людей очень, очень мало, но именно благодаря их действиям вы сейчас можете видеть эти уроки.

Со своей стороны выражаю большую благодарность спонсорам. Ваша поддержка даёт мне силы продолжать.

← ПРЕДЫДУЩИЙ УРОК   СЛЕДУЮЩИЙ УРОК →